隐含赔率的可视化

隐含赔率是扑克理论中的一个关键指标。你可能听说过这个术语，并且对这个概念有了基本的了解，然而，在求解器时代，这个概念已经有了很大的发展。

什么是隐含赔率？

隐含赔率是指你期望获得的超过原始权益的价值。你可以把它理解为当你击中补牌并反超对手时，你期望在未来几条街获得的价值。 这个概念与“直接底池赔率”形成对比，用来解释为什么有些牌即使没有足够的原始权益跟注也能盈利地追牌。

直接赔率 vs 隐含赔率

这里有一个例子。我们在转牌圈面对一个 10BB 底池大小的赌注。我们拿着一个胜率为 25% 的听牌。我们应该跟注吗？

直接底池赔率计算

直接底池赔率是指为了至少在跟注时不亏损，你需要赢得牌局的百分比。这假设之后没有更多的钱进入底池。

• 25% 的情况下我们击中听牌并赢得 20BB（底池 + 对手的赌注）
• 75% 的情况下我们错过听牌并输掉 10BB（我们的跟注）

跟注的期望值 = (25% x 20BB) – (75% x 10BB) = 5 – 7.5 = -2.5BB

显然，这是一个亏损的跟注。然而，这种计算的问题在于它忽略了之后进入底池的钱——这就是隐含赔率发挥作用的地方！

隐含赔率计算

为了证明这个跟注是合理的，我们需要在河牌圈赢得一些额外的钱 (M)。如果我们错过听牌，我们总是可以弃牌。

• 25% 的情况下我们击中听牌并赢得 20BB + M（底池 + 对手的赌注 + M）
• 75% 的情况下我们错过听牌并输掉 10BB（我们的跟注）

跟注的期望值 = (25% x (20+M)) – (75% x 10)

为了达到盈亏平衡，当我们击中听牌时，我们需要额外赢得多少钱？将期望值设为零以找到盈亏平衡点，然后求解 M：

0 = (25% x (20+M)) – (75% x 10) M = 10

我们需要在河牌圈平均多赢 10BB 才能证明跟注是合理的。 这相当于在河牌圈下一个 ⅓ 底池大小的赌注。所以如果我们认为当我们击中听牌时，我们至少可以榨取一个 ⅓ 底池大小的赌注，那么这个跟注就变得有利可图了！

换句话说，一个跟注“隐含”着它将在河牌圈赢得（至少）额外的 10BB。这就是这个术语的由来。

它与权益实现的关系

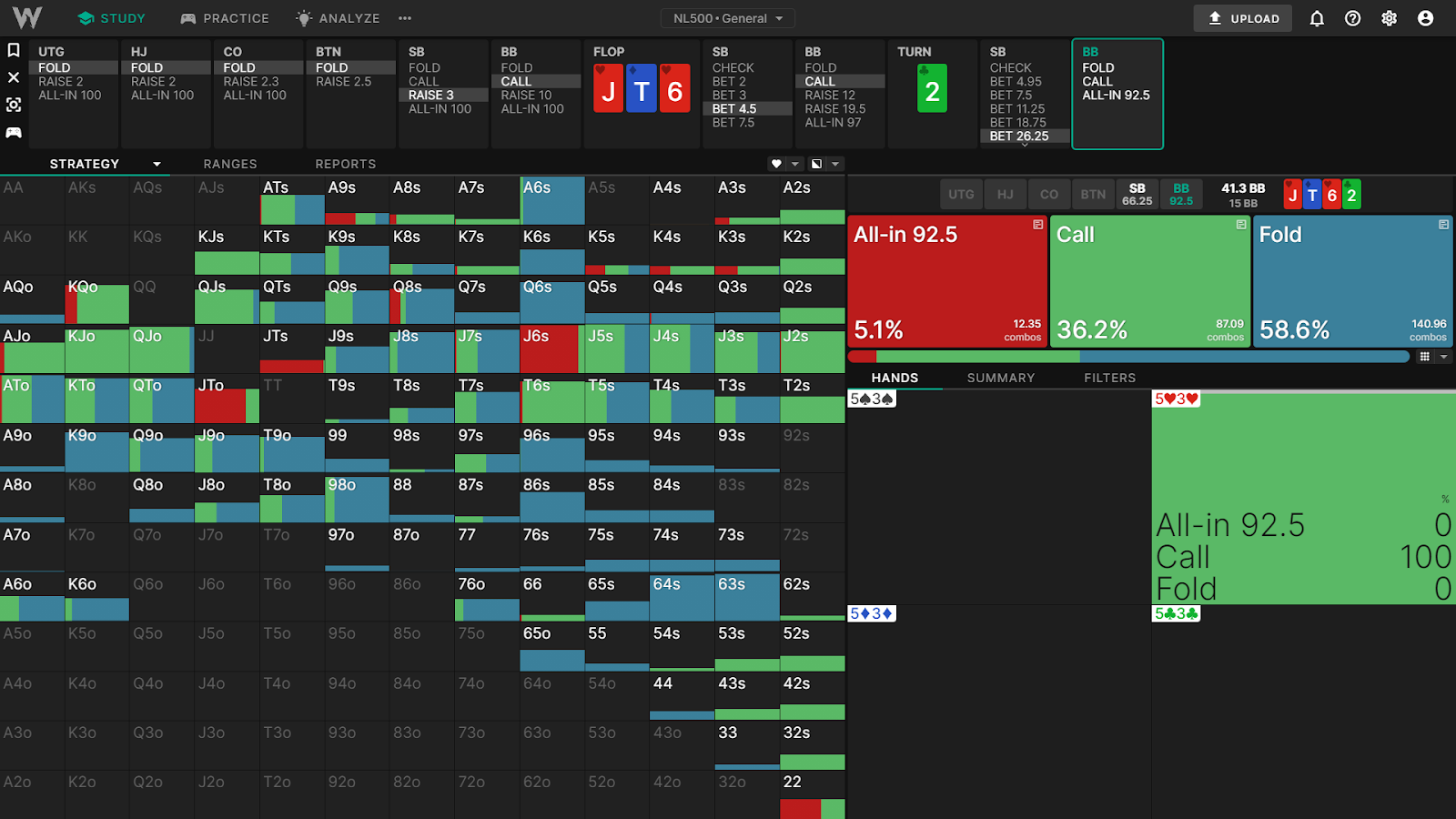
小盲注开局，大盲注跟注。翻牌是 J♥T♦6♥2♣。小盲注下注 75%，大盲注跟注。小盲注在转牌圈过牌加注 175% 底池，大盲注拿着 5h3h 行动。

让我们从一个简单的底池赔率计算开始。我们（大盲注）面对一个 26.25BB 的赌注，底池是 15BB。为了在跟注时不亏损，我们长期来看至少需要赢得 26.25BB。

假设我们拿着一个边缘的卡顺听牌，比如 5♥3♥，它的胜率只有 31.68%。让我们看看我们的直接底池赔率。所需的权益 = (跟注金额) / (跟注后的底池 – 佣金)。大盲注需要 26.25 / (15 + 26.25*2 – 0.6) = 39.24% 的权益才能跟注。

如果小盲注全押（或者如果河牌圈总是过牌到底），这将是一个很容易的弃牌。然而，跟注后还有 66.25BB 的筹码。由于隐含赔率，5h3h 预计在击中听牌时会赢得超过其公平份额的权益。

我们拿着 5h3h 的期望值比弃牌高 5.33BB。这实际上意味着，我们预计在跟注后会赢得 (26.25BB + 5.33BB = 31.58BB)。在我们跟注后，底池将是 67.5BB，所以我们预期的底池份额是 (31.58 / 67.5) = 46.78% 底池（忽略佣金）。

让我们回顾一下：

• 我们的原始权益是 31.68%
• 我们的底池份额是 46.78%

换句话说，我们过度实现了我们的权益：46.78/31.68 = 148%

更准确地说，我们的期望值高于我们的原始权益所暗示的值，因为我们有能力在以后的几条街赢得更多的价值。这就是隐含赔率的本质。

反向隐含赔率

反向隐含赔率也存在。例如，有时你会击中你的听牌，但仍然会输掉一个巨大的底池。有时，一手成牌不会赢得其公平份额的底池，因为它在后面的几条街被压制或反超。拿到第二好的强牌会严重削减你的利润空间。

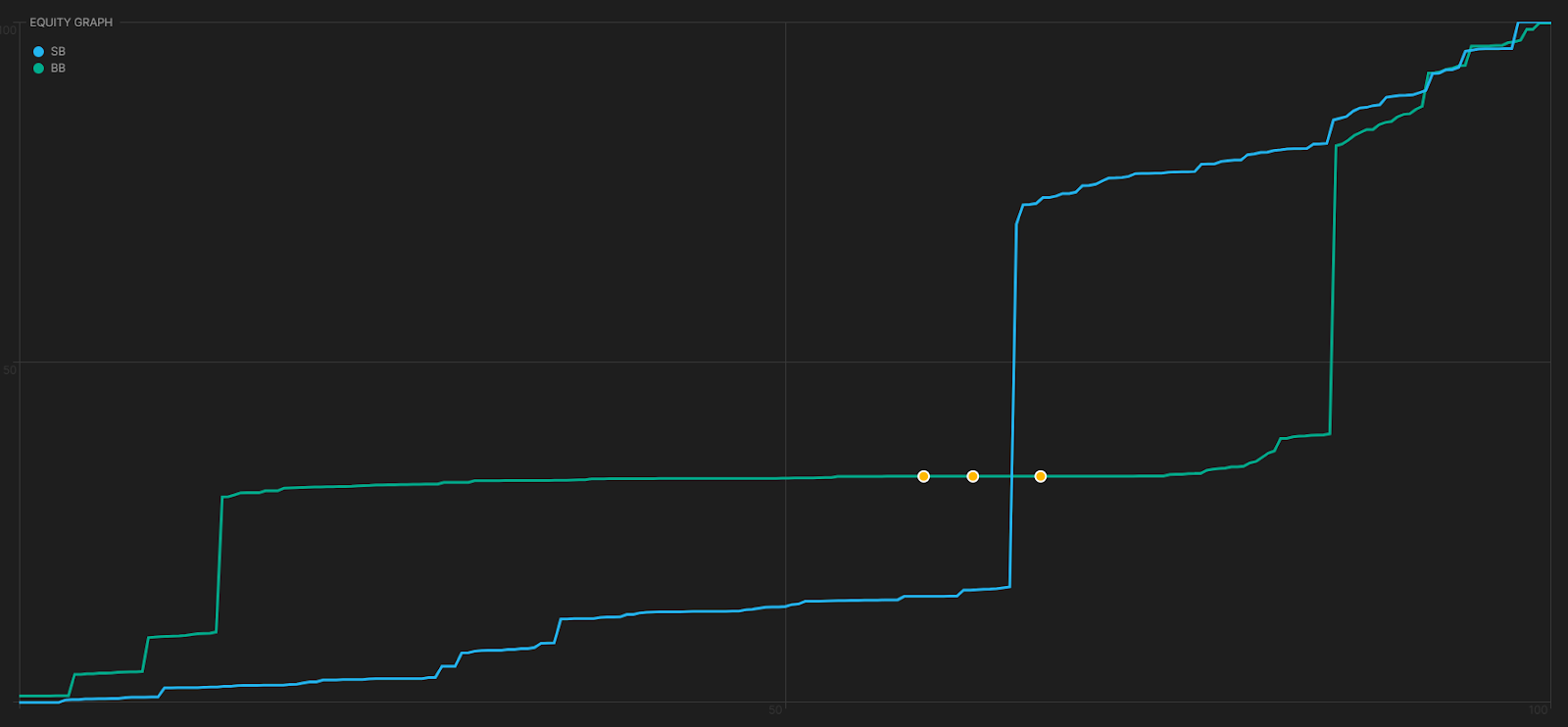
让我们回到我们最初的 J♥T♦6♥2♣ 例子，假设我们拿着 K♠J♠。

K♠J♠ 拥有良好的权益，并且领先于对手范围的一半以上。然而，它面对他们的过牌加注几乎没有超过盈亏平衡点。当你的对手范围两极分化时，你的边缘成牌很难反超对手的价值牌。这些牌更像是诈唬捕捉牌，并且具有较差的反向隐含赔率。

同样，我们需要赢得 26.25BB 才能达到盈亏平衡，而 K♠J♠ 赢得了 26.25 + 2.21 = 28.46BB，或者大约 28.46/67.5 = 42% 的底池。

原始权益：54.71% 期望值：42.16% 权益实现 = 77%。

换句话说，我们只实现了 77% 的原始权益。

那么我们剩下的期望值去了哪里呢？好吧，小盲注有能力过度实现他们的权益，并在河牌圈让我们的一对顶对处于很多无差异的局面。他们可以用更强的价值牌/诈唬牌在我们面前两极分化，反超我们，并用我们的一对顶对获得巨额利润。我们不可能跟注每一个河牌圈的赌注。我们有一个诈唬捕捉牌，它不能从更差的牌中榨取价值，因为他们的范围太强了。

让我们将其可视化。这是我们面对他们过牌加注时的权益分布。线上的点代表我们所有的 KJs。正如你所看到的，大多数大盲注的范围是无差异的，正如那条长长的诈唬捕捉牌的平线所示。

隐含赔率与筹码深度之间的关系

筹码深度是评估隐含赔率时最大的单一因素。请记住，“隐含”表示我们期望在后面的几条街赢得额外的筹码。我们身后的筹码越多，在后面的几条街赢得（或输掉）筹码的可能性就越大，隐含/反向隐含赔率也就越高。

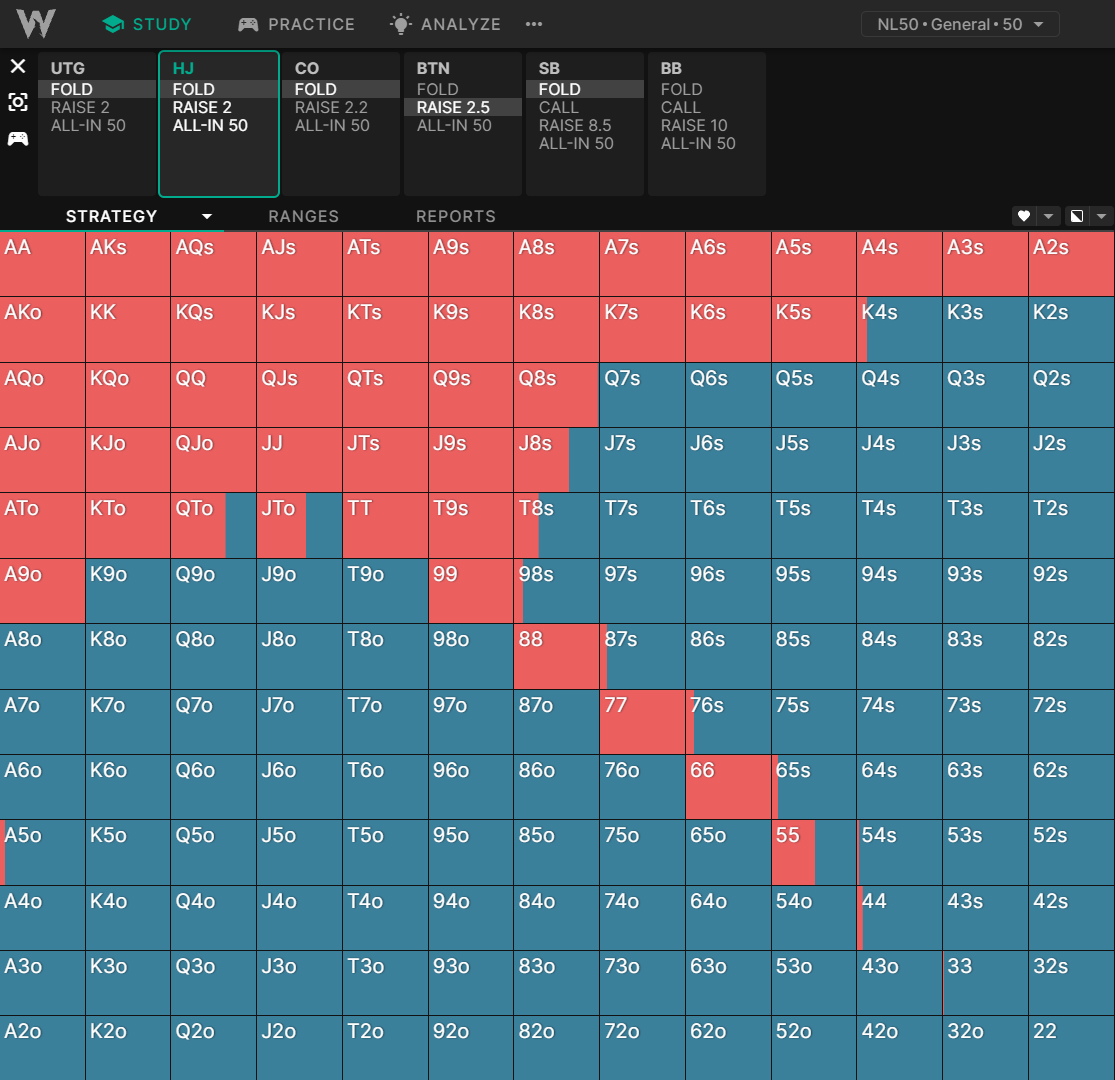
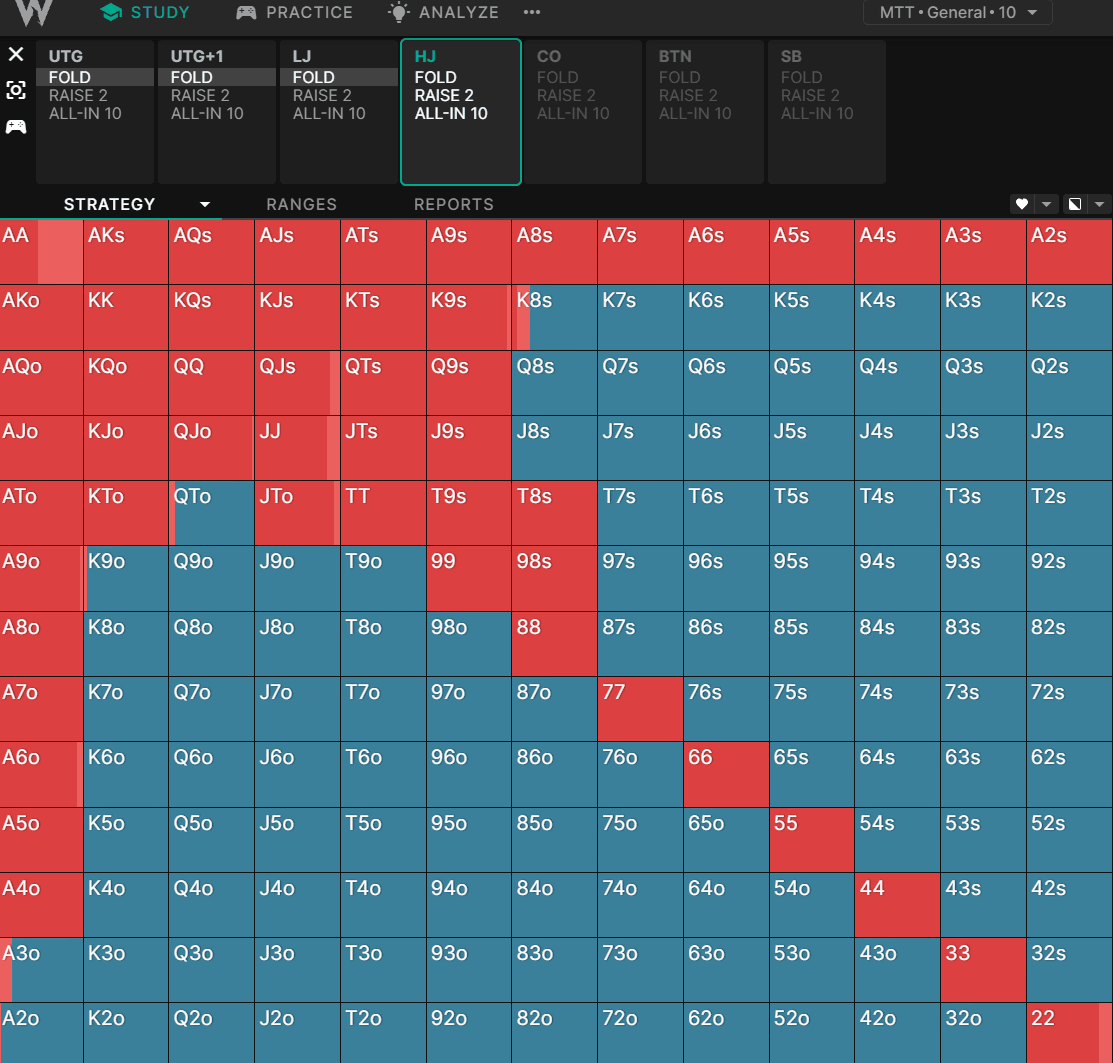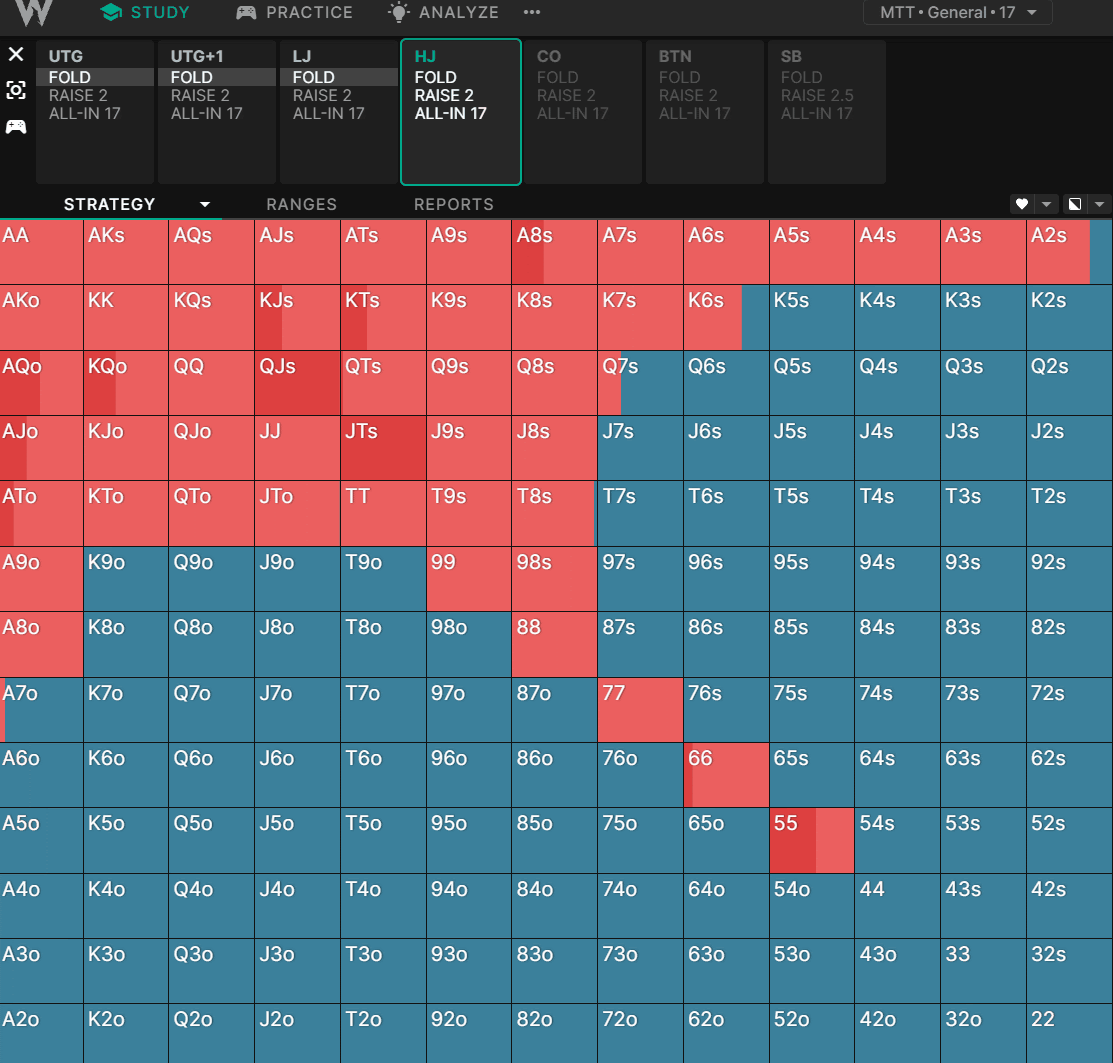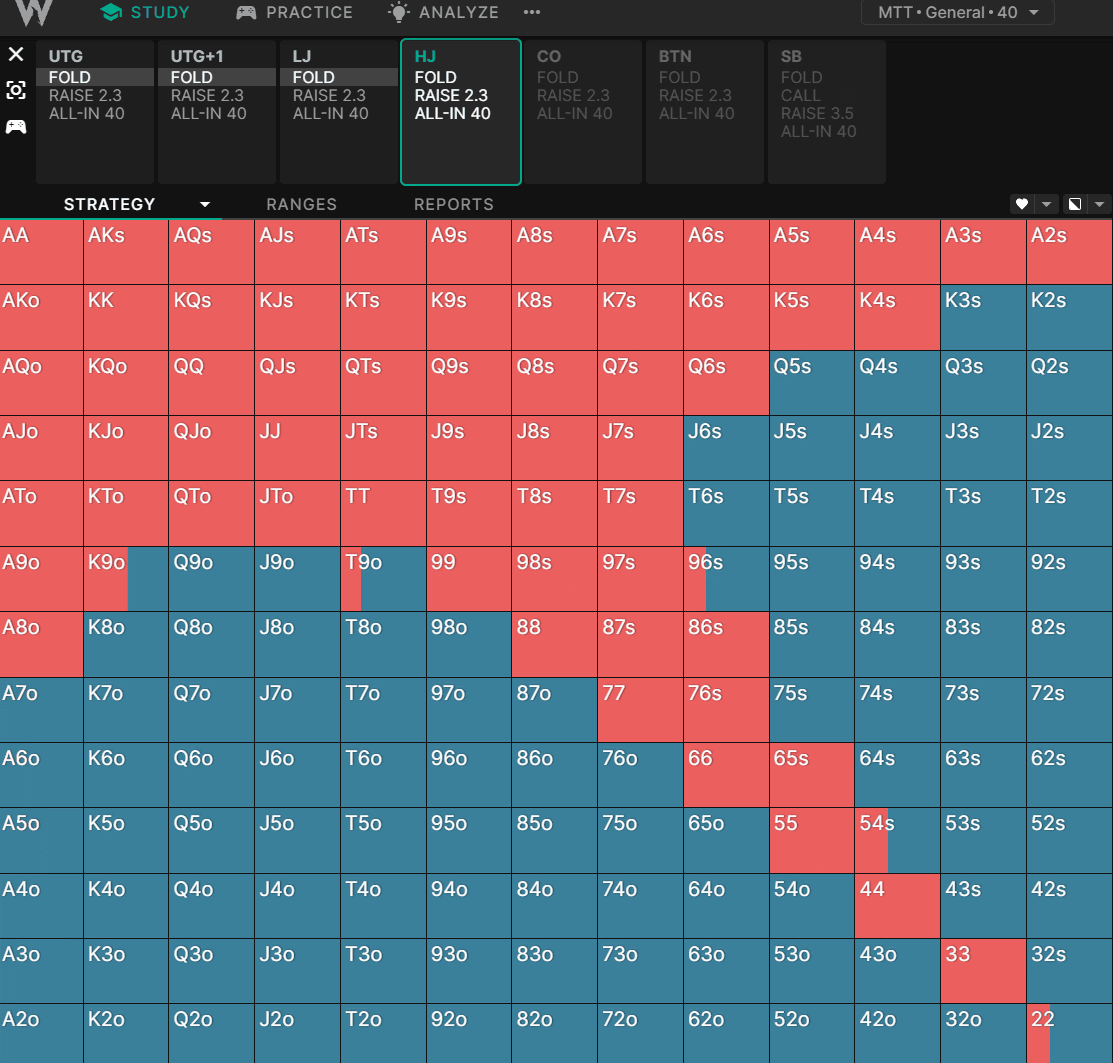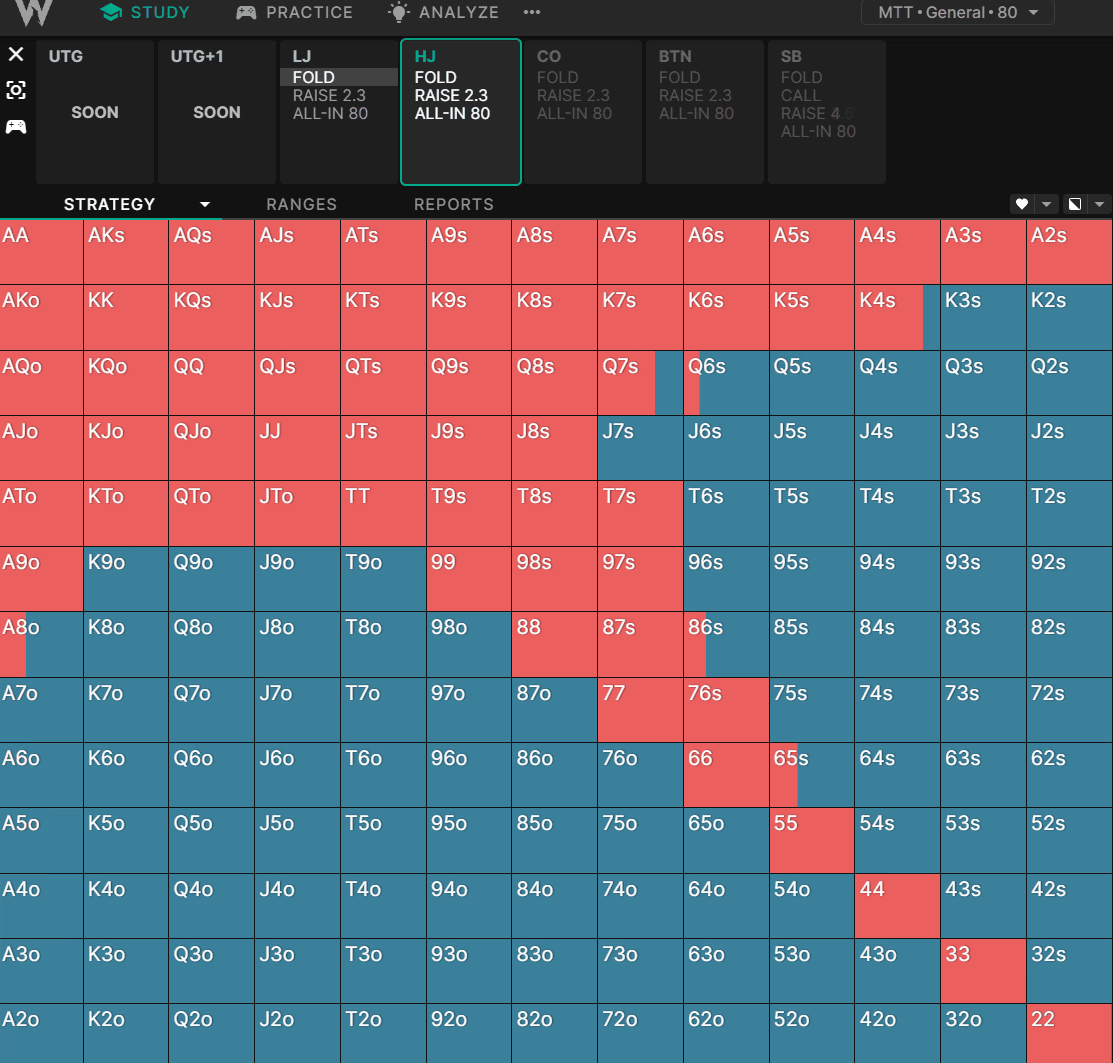
让我们比较一下求解器在标准现金游戏中如何在不同的筹码深度下打开枪口位置：

枪口位置开局：50BB 深度

你还应该考虑你的对手在后面的几条街投入筹码的可能性有多大。例如，如果他们在所有同花完成的转牌和河牌上都停止下注，那么你的同花听牌的隐含赔率就会降低。

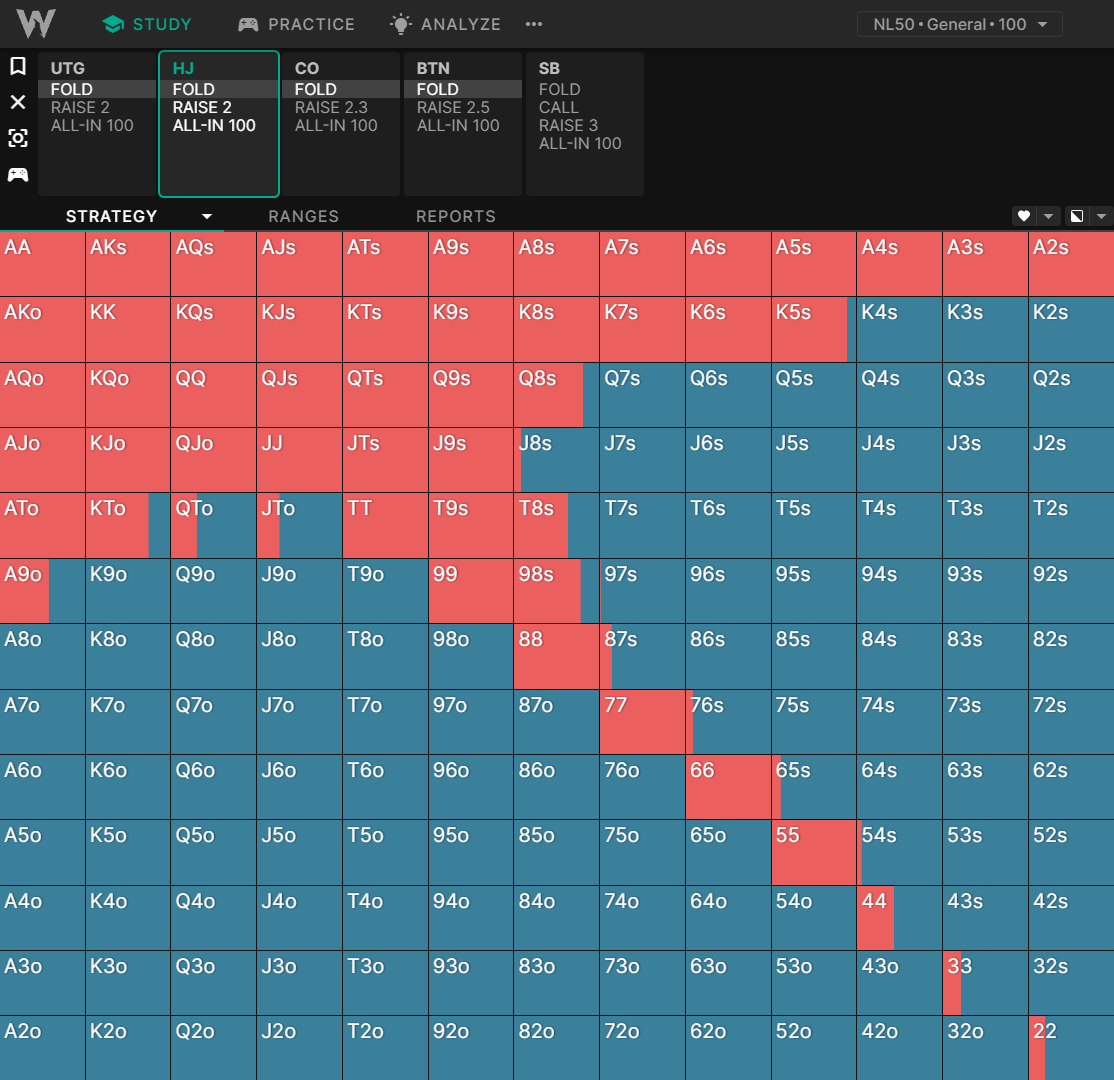
枪口位置开局：100BB 深度

随着我们筹码越来越深，我们看到对诸如较小的口袋对子、同花连牌以及通常具有更好隐含赔率的牌的偏好。这种影响是微妙的，但在锦标赛图表中更加明显：

我们可以看到，范围从低筹码深度的高权益全押扩展到更深筹码深度下具有更好隐含赔率的更“可玩”的牌。当其他玩家由于隐含赔率的提高而可以用更广泛的范围进入底池时，范围在 60BB+ 时会缩小。

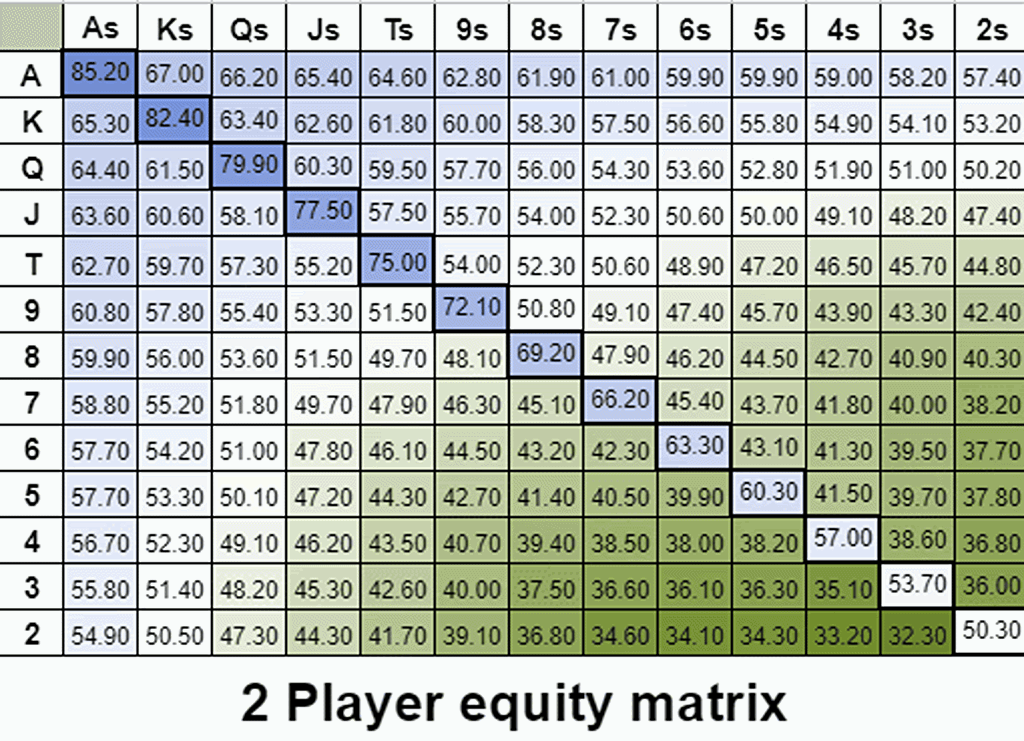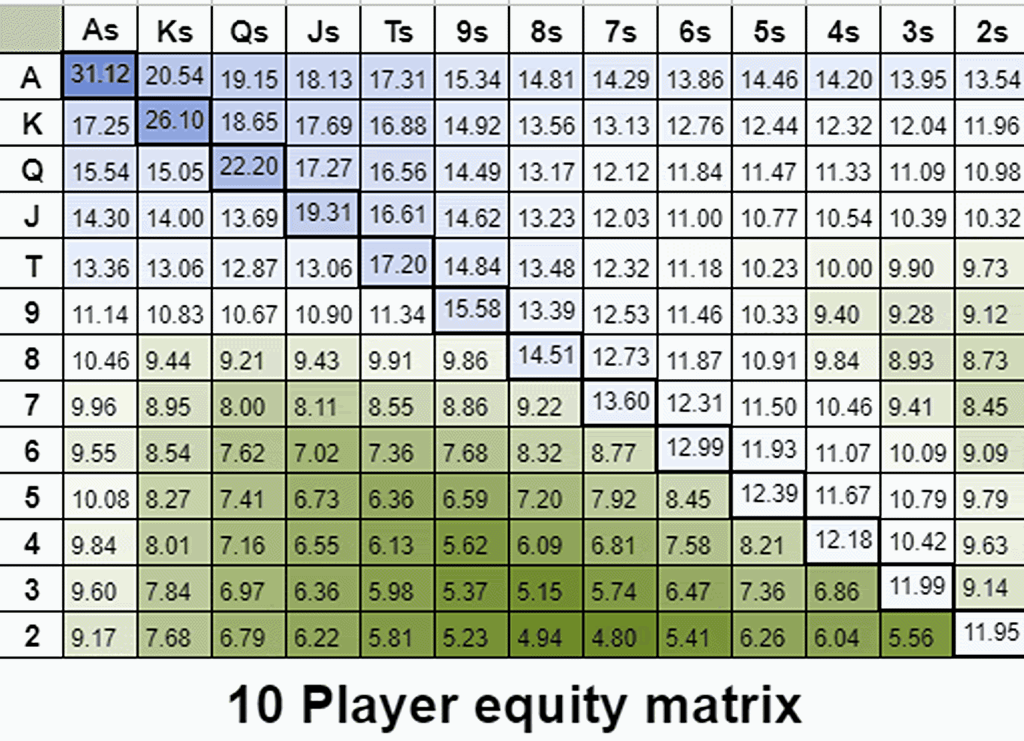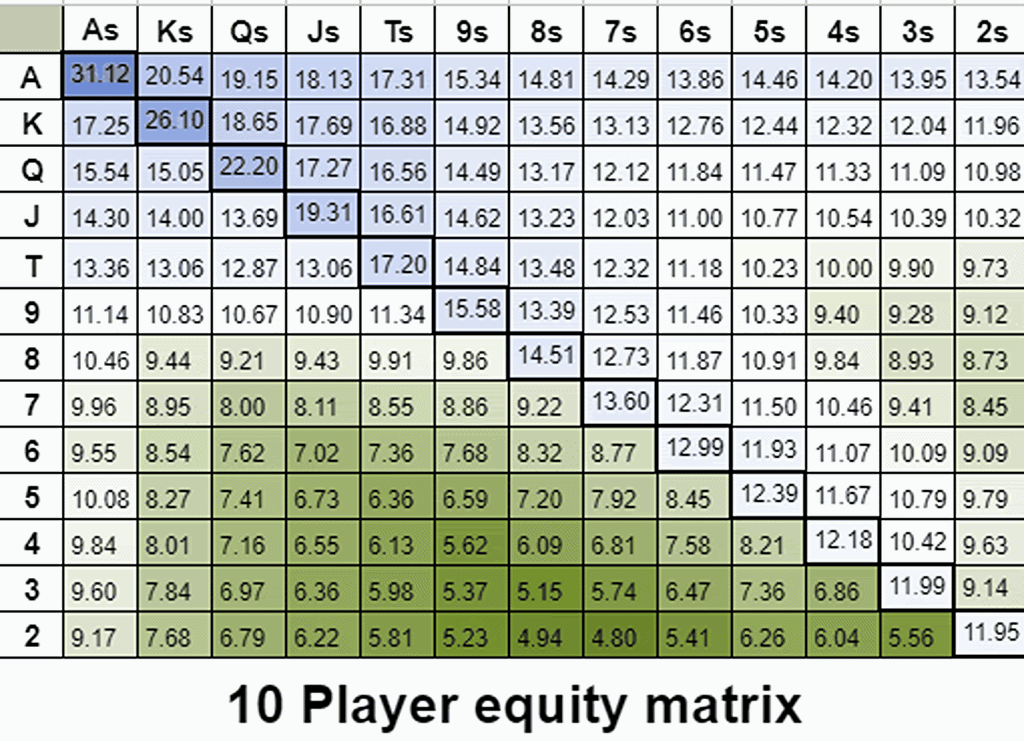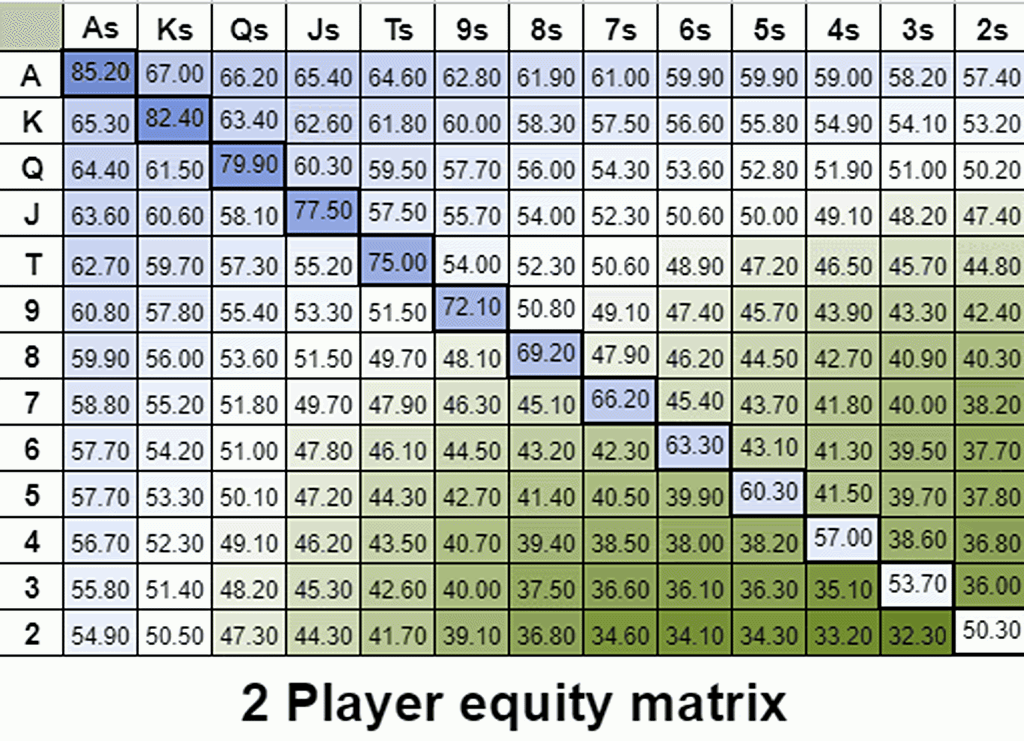
通过多路权益保留可视化隐含赔率

隐含赔率与一手牌能够抽到坚果牌的能力有关。我们有时称这种效应为“可玩性”。下面的动图是 2-14 名玩家拿着任意两张牌的彩色编码权益分布。在这里，我们可以看到权益是如何在多路情况下演变的。请注意渐变而不是确切的数字。

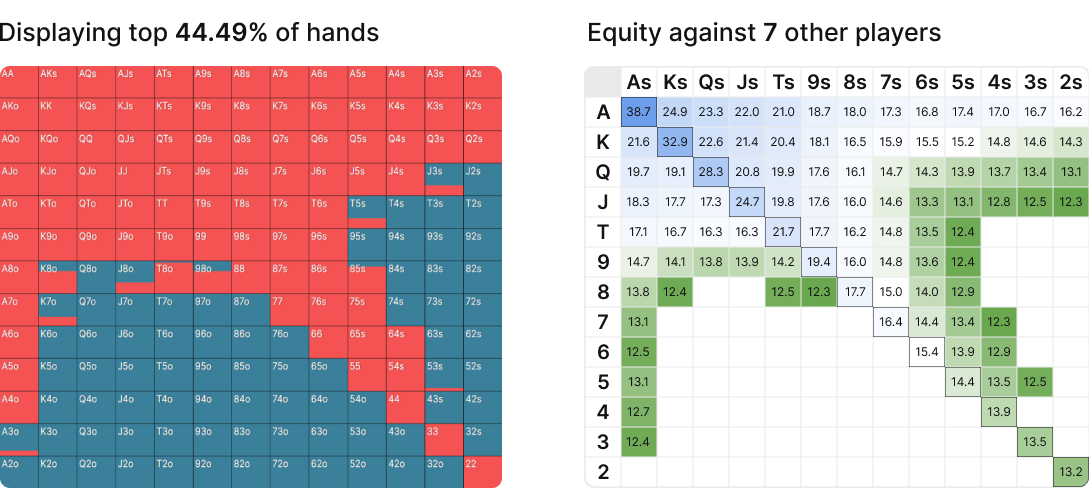
令我惊讶的是，我发现通过调整玩家数量（调整隐含赔率的值），你可以创建大致类似于 GTO 开局范围的权益梯度。例如，以下是前 44% 的牌在标准 100BB 按钮位置开局范围旁边的权益梯度。

自己试试这个电子表格！

即使牌局中只剩下 3 名玩家，隐含赔率的价值在 100BB 深度时也会被夸大。为了复制 GTO 期望值梯度，我通过将多路权益计算增加到 8 名玩家人为地增加了隐含赔率。

随着我们添加更多玩家，权益梯度会向更适合和连接的牌转移，这些牌有更好的机会抽到坚果牌。

通过这种方式，我们将隐含赔率视为一个可调整的参数，以人为地突出不同类型牌的内在隐含赔率（或者更准确地说，一手牌抽到强牌的内在能力）。

即使牌局中只剩下 3 名玩家，隐含赔率的价值在 100BB 深度时也会被夸大。为了复制 GTO 期望值梯度，我通过将多路权益计算增加到 8 名玩家人为地增加了隐含赔率。这种分析低估了阻断效应，这使得复制早期位置开局范围变得更加困难。无论如何，我希望你和我一样喜欢这种隐含赔率的可视化表示！

GTO Wizard 扑克玩家的首选应用程序

研究任何可以想象的局面

通过与 GTO 对战进行练习

一键分析你的牌局

立即开始碾压加入 DISCORD

作者

Tombos21

Tom 是一位资深的扑克理论爱好者，GTO Wizard 教练和 YouTuber，以及《每日 GTO 剂量》的作者。