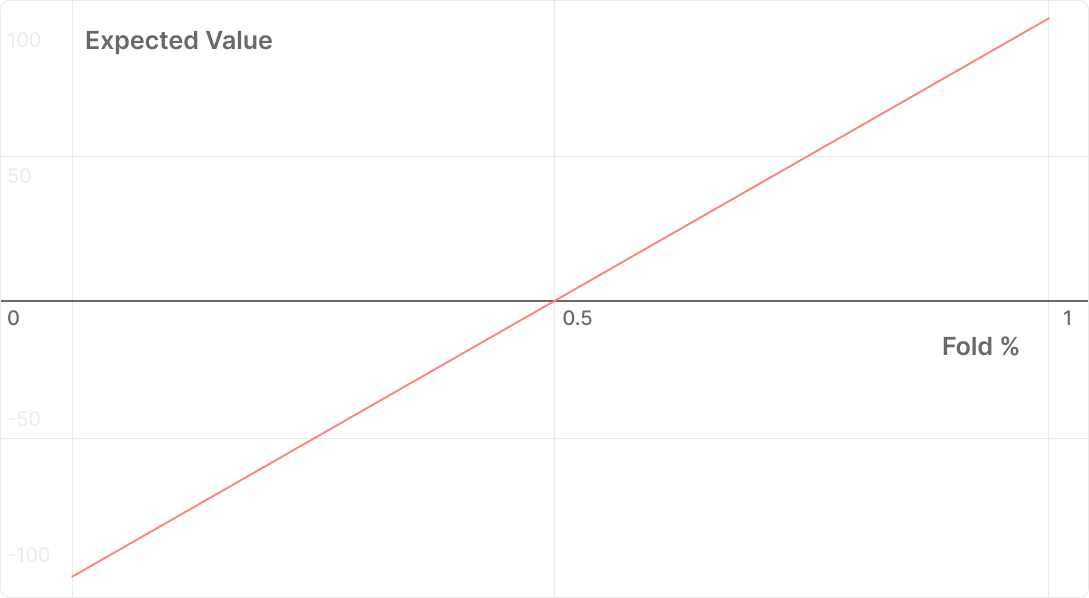最小防守频率和Alpha值

最小防守频率 (MDF) 和 Alpha 值是扑克中的指标，用于确定面对特定下注大小需要防守的范围宽度。

如果你的防守范围过宽，那么你的对手可以通过价值下注来剥削你。如果你的防守范围过窄，那么他们可以通过诈唬来压制你。因此，一个好的策略是跟注足够多的牌，使诈唬变得无利可图。

这个指标在实践中存在一些问题，但它是扑克理论中的一个重要概念。

什么是最小防守频率？

最小防守频率是一种衡量标准，它告诉你需要多高的频率跟注才能使对手的 0% 胜率牌在诈唬和放弃之间无差异。

MDF 简单来说就是确保你的对手不能用任何两张牌进行有利可图的诈唬。你需要防守最低频率，以防止被诈唬压制。

MDF 是一种风险/回报计算，旨在使对手的诈唬期望值为 0。

什么算作“防守”？

防守意味着继续游戏。你可以通过加注或跟注来防守。两者都算作防守。

关于 MDF 的警告

MDF 应该被视为防止对手过度诈唬的盾牌！首先，我们需要明确这一点。

如果你的对手诈唬得不够多，请不要使用 MDF。

如果他们明显诈唬不足，那么试图使他们的诈唬期望值为 0 是没有意义的。放下你的盾牌，拥抱面对价值型对手的过度弃牌。 MDF 应该仅仅被用作防止他们用诈唬压制你的盾牌。

什么是 Alpha 值？

如果最小防守频率 (MDF) 是你的盾牌，那么 Alpha 值 (α) 就是你的剑！

Alpha 值是逆向计算。它告诉你你的对手需要弃牌的频率，才能使你的 0% 胜率诈唬至少达到盈亏平衡。

**Alpha 值是一种风险/回报计算，旨在计算你的对手需要防守多高的频率才能使你的诈唬达到盈亏平衡。**如果你认为他们防守的频率较低 - 太好了！如果他们防守的频率较高，也许需要重新考虑你的诈唬。

Alpha = 1 – MDF MDF = 1 – Alpha

计算

公式

这种风险/回报计算考虑下注大小相对于底池的大小，以计算使诈唬无差异所需的总体防守频率。

计算 MDF/α 的公式非常简单。

Alpha (α) = 风险 / (风险 + 回报) 其中： 风险 = 你在诈唬时冒的风险金额 回报 = 他们弃牌时你获得的金额

你还可以使用另一个公式，它考虑了下注和底池大小。我不喜欢这个公式，因为它不适用于加注，它只适用于初始下注。但我还是把它放在这里供你参考。

MDF = 底池 / (下注 + 底池) Alpha = 下注 / (下注 + 底池)

示例 1

你在 100 美元的底池中下注 60 美元。求 Alpha 值和 MDF：

• 风险 = 60 美元（你在诈唬时冒 60 美元的风险）
• 回报 = 100 美元（他们弃牌时你获得的金额）

Alpha (α) = 风险 / (风险 + 回报) Alpha (α) = 60 美元 / (100 美元 + 60 美元) Alpha (α) = 37.5%

你的对手需要至少 37.5% 的时间弃牌才能使你的诈唬达到盈亏平衡。

MDF 简单来说就是 1 – α

在这种情况下，MDF = 1 – 37.5%，结果是 62.5%。**因此，对手需要至少防守 62.5% 的范围才能使你的诈唬达到盈亏平衡。**如果他们防守的频率低于此值，你的诈唬将是有利可图的，如果他们防守的频率高于此值，你的诈唬将亏损。

示例 2

你在 100 美元的底池中下注 60 美元，你的对手加注到 200 美元。你的 MDF 和他们的 Alpha 值是多少？

你的对手冒了 200 美元的风险来赢得 (100 美元 + 60 美元) 的底池

Alpha (α) = 风险 / (风险 + 回报) Alpha (α) = 200 美元 / (200 美元 + 160 美元) Alpha (α) = 55.5% MDF = 1 – α = 44.5%

因此，你需要防守 44.5% 的下注范围来应对加注，以防止他们用任何两张牌进行有利可图的诈唬加注。相反，他们需要你至少弃牌 55.5% 的下注范围才能进行有利可图的纯诈唬。

速查表

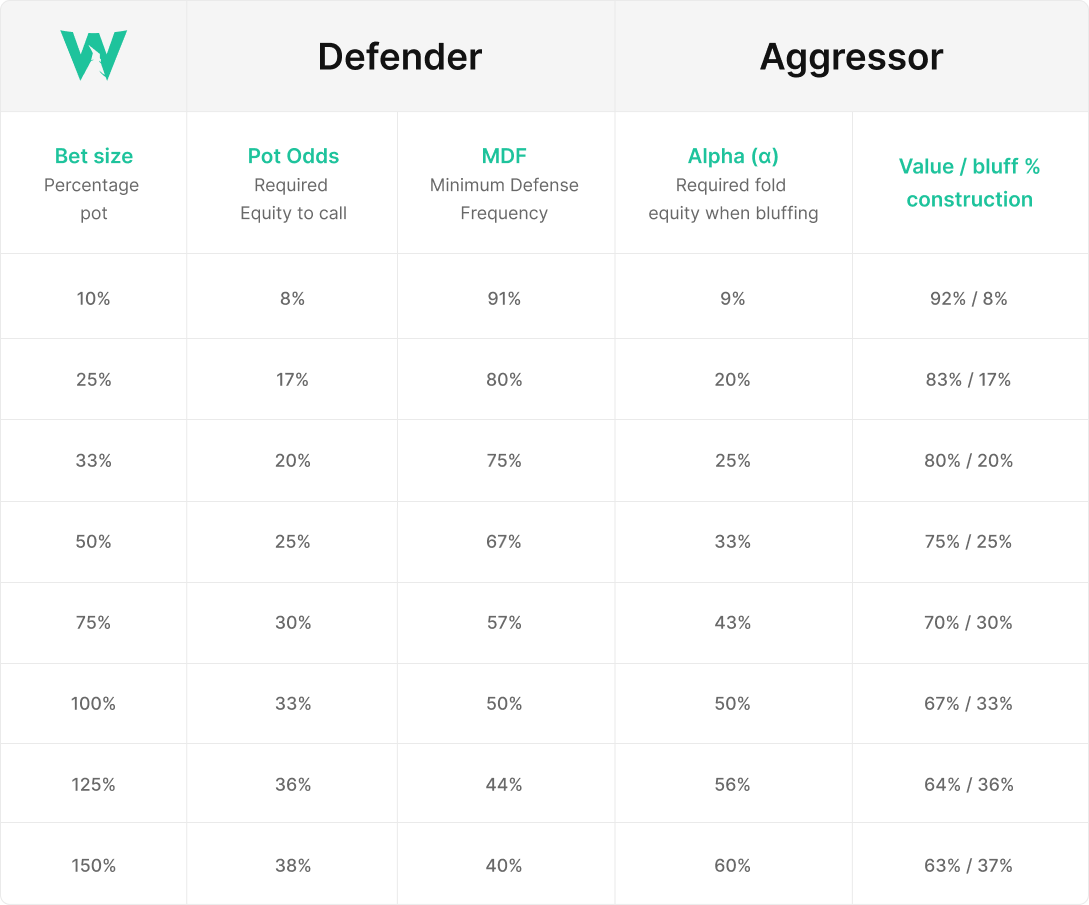
有些玩家只是简单地使用速查表来估计面对下注大小的 Alpha 值和 MDF。为了方便起见，我们在这里制作了这样一个速查表！要使用此图表，只需查看第一列中的下注大小，并在第三/第四列中找到相应的 Alpha 值/MDF。

免责声明 - 这些数字仅适用于初始下注！面对加注时，MDF 和 Alpha 值会发生变化，并且不能仅用下注大小作为底池百分比来确定。

期望值计算

MDF 和 Alpha 值只寻找盈亏平衡点。我们可以使用一个简单的期望值公式来计算纯诈唬的实际盈利能力。这也能让我们根据他们跟注的范围宽度来衡量盈利能力的范围。

纯诈唬的期望值可以写成如下：

EV（诈唬）= (弃牌% x 底池) – (跟注% x 下注)

这是因为底池是我们弃牌时获得的金额，而我们的下注是我们跟注时损失的金额。现在，我们假设我们的诈唬在被跟注时总是会输。

示例 3

我们在河牌圈用纯诈唬进行 125% 底池的超额下注。我们的对手跟注 40% 的范围。为了方便计算，我们假设底池是 100 美元。

EV（诈唬）= (弃牌% x 底池) – (跟注% x 下注) EV（诈唬）= (60% x 100 美元) – (40% x 125 美元) = 10 美元 所以这个诈唬的期望值是 10 美元，因为我们的对手过度弃牌了！

那么他们需要弃牌多高的频率才能使我们的诈唬价值 0 美元呢？ Alpha = 风险 / (风险 + 回报) = 125 / 225 = 55.5%

换句话说，如果他们防守 44.5% 的范围，这个超额下注诈唬将达到盈亏平衡。但因为他们稍微过度弃牌，所以它变得有利可图了！

图表

让我们用图表 来表示我们诈唬的盈利能力与他们弃牌百分比的关系：

• 他们弃牌越少（左），我们的诈唬损失的钱就越多（下），最多达到我们冒的风险金额。
• 他们弃牌越多（右），我们的诈唬就越有利可图（上），最多达到底池的金额。

从几何角度来看，我们可以在 (0, -125) 和 (1, 100) 之间画一条直线，这条线与 x 轴的交点表示我们的诈唬达到盈亏平衡所需的弃牌百分比。在这个例子中，这个交点正好是 Alpha 值，即 55.5%。

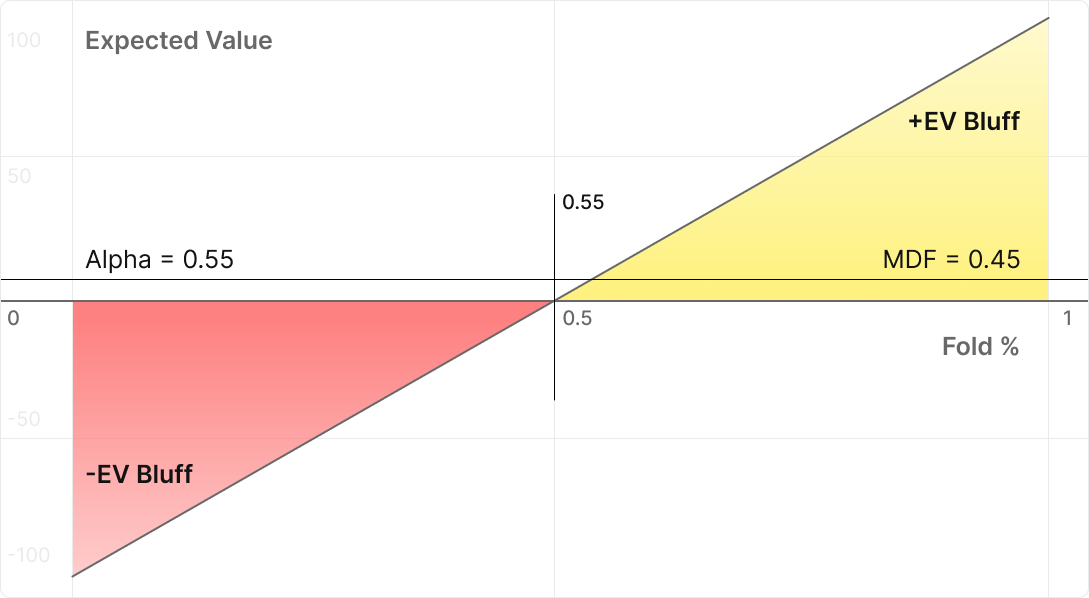
让我们给这个图表上色。

在右边我们可以看到 +EV 区域，我们的对手弃牌的频率超过 55%。在左边我们可以看到 -EV 区域，他们弃牌的频率低于 55%。

局限性

让我们来谈谈一个显而易见的问题。事实是，MDF 在真空中并不能很好地发挥作用。MDF 做了一个主要的假设，限制了它作为一个独立指标的实用性。

MDF 假设诈唬没有胜率。

这在大多数情况下并不反映现实。在真实的扑克中，诈唬在河牌圈之前通常会有一些胜率。

例如，你可以用听牌进行半诈唬 - 即使是静态的高牌也比对手价值区域中的一部分牌强。

那么这会如何改变情况呢？

当过牌有胜率时

当诈唬作为过牌有胜率时，你不再试图使它们的价值为 0 美元。相反，你的目标是使这些诈唬在下注和过牌之间无差异！

**例如，如果你的对手在河牌圈用成手牌诈唬，你应该只对那些可以击败诈唬的牌应用 MDF。**对那些不是诈唬捕捉手的牌应用 MDF 是没有意义的，因为它们无论如何都会输给过牌。

示例

对手在河牌圈的位置下注全底池。他们的诈唬作为过牌将有 20% 的胜率。你应该防守多宽的范围才能使他们的诈唬无差异？

**你的目标是使诈唬的期望值等于过牌的期望值。**我们知道过牌的期望值是 20% 的底池。

诈唬的期望值 = 0.2 (底池) = (弃牌% x 底池) – (跟注% x 下注) 0.2 = (1-跟注%) – 跟注% 跟注% = 40%

如果这是一个 0% 胜率的诈唬，我们会跟注 50%。但是，由于他们的诈唬有价值，我们可以过度弃牌，只防守 40% 的 MDF。换句话说，我们可以让他们进行有利可图的诈唬，因为他们的诈唬作为过牌有胜率。

我们的目标是使他们的诈唬期望值 = 过牌期望值 过牌期望值 = 20% 底池 诈唬期望值 = 20% 底池（如果我们防守不足）

简而言之：当他们用摊牌价值诈唬时，要防守不足

当诈唬在面对跟注时保留胜率时

对手在转牌圈下注全底池。他们的诈唬完全是听牌，在面对你的跟注范围时保留 20% 的胜率。用这些听牌过牌转牌圈的期望值也是 20% 的底池。你应该防守多宽的范围才能使这些听牌在下注和过牌之间无差异？

你的目标是使诈唬的期望值等于过牌转牌圈的期望值。我们知道过牌的期望值是 20% 的底池。

EV（诈唬）= EV（过牌）= 20% 底池

我们需要修改期望值方程式，以包括他们在被跟注时的胜率： 0.2 = (弃牌% * 底池) + 跟注%((赢牌% * (下注 + 底池)) – (输牌% * 下注)) 0.2 = (1 – 跟注%) + 跟注% (20% * 2 – 80%) 跟注% = 57%

一种更直观的解释是，听牌作为诈唬的风险较低（与纯诈唬相比），因为它们在被跟注时有胜率。

用 20% 听牌进行底池大小的下注，其风险/回报比率与用纯（0% 胜率）诈唬进行 75% 底池的下注大致相同。从这个意义上说，这几乎就像下注变小了一样。这与为什么你经常可以在听牌多的牌面上下注更大的原因有关。然而，在实践中，你很少会试图使强听牌无差异。

GTO 是否遵循 MDF？

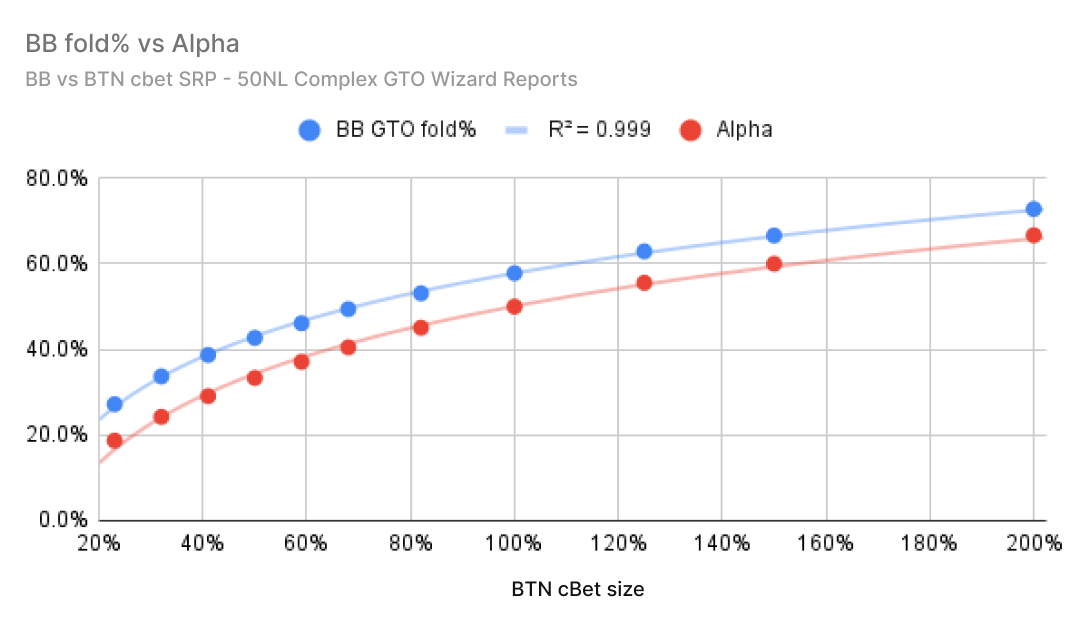
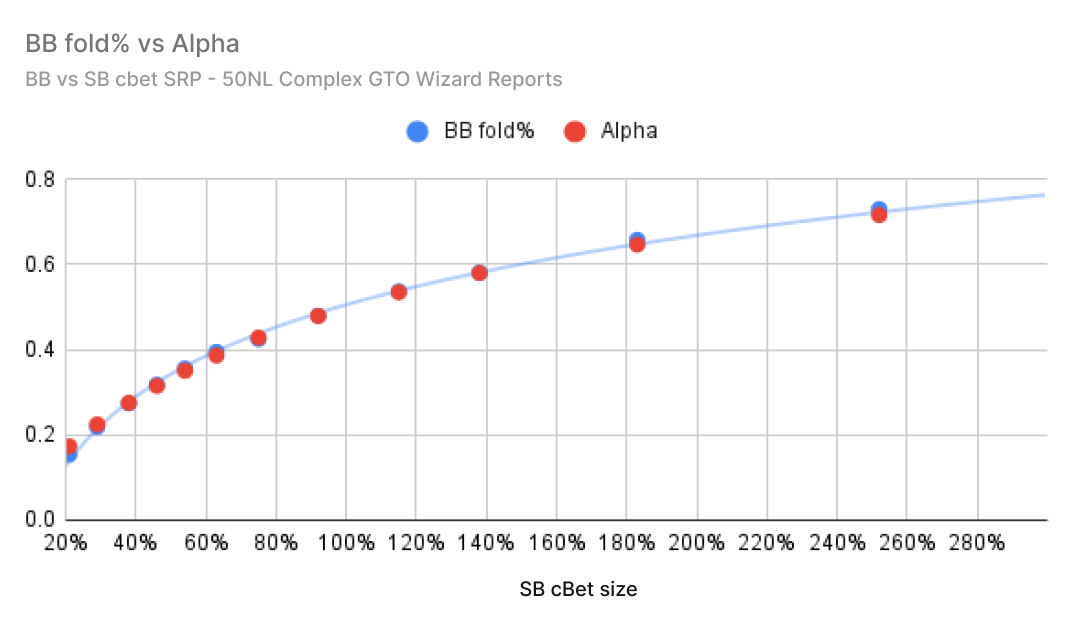
使用 GTO Wizard 的复杂报告，我绘制了 GTO 弃牌频率（蓝色）与假设的 MDF 弃牌频率（红色）的图表。这些报告涵盖了所有 1755 个策略上不同的翻牌圈。平均而言，大盲注在翻牌圈对所有下注大小都持续过度弃牌。

按钮位 vs 大盲注 复杂报告

以下是针对小盲注 vs 大盲注单挑底池的相同报告。在这种情况下，防守方有位置优势，因此平均而言，跟注更接近 MDF。

小盲注 vs 大盲注 复杂报告

防守不足

相对于 MDF 的防守不足在理论上很常见，事实上在很多情况下是首选策略。根据 MDF 跟注的问题在于，你剥夺了对手诈唬那些过牌期望值大于 0 的牌的动机。

这在只有坚果牌/空气牌的玩具游戏中不是问题，但在真实的扑克中，诈唬有胜率，这是一个问题。在大多数情况下，防守不足的漏洞几乎肯定比过度防守少！

一般来说，在以下情况下，你应该比 MDF 防守得少：

• 你在翻牌圈或转牌圈处于不利位置（有利位置的诈唬在过牌时有期望值）
• 当对手用成手牌诈唬时（只对那些可以击败诈唬的牌应用 MDF）
• 当对手的过牌有期望值时
• 策略性地，针对价值型对手

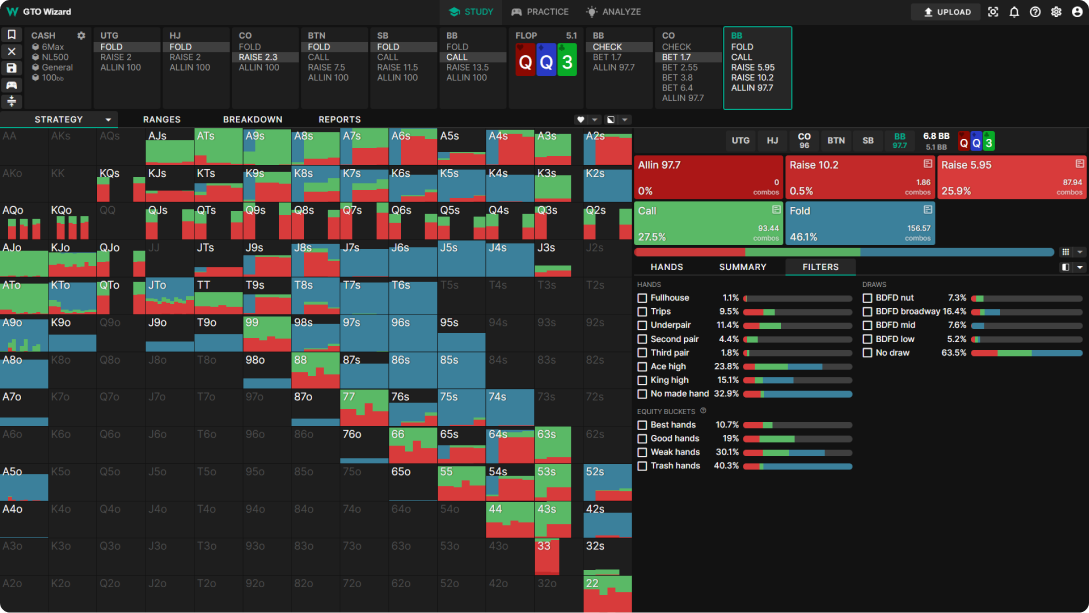
这里有一个例子。这是 QQ3r 翻牌圈上的庄家位 vs 大盲注单挑底池。按钮位的大多数诈唬在这张牌面上都有很大的胜率和期望值。此外，大盲注根本无法实现他们的胜率。因此，大盲注需要在这张翻牌圈上大幅过度弃牌。

庄家位持续下注 33% 底池。大盲注的 MDF 说他们应该防守 75% 的范围，并且面对这个下注大小最多弃牌 25%。然而，求解器过度弃牌，几乎弃掉了它一半的范围！

过度防守

相对于 MDF 的过度防守非常罕见，但它在理论上确实有其地位。一般来说，我们会在侵略者的诈唬在面对跟注范围时保留胜率的情况下看到过度防守。策略性地，当你的对手过度诈唬时，你可以选择过度防守。

一般来说，你应该在以下情况下过度防守：

• 在听牌多的牌面上进行早期全押
• 在有利位置，当对手用保留胜率的听牌诈唬时
• 在平分底池的牌面上
• 策略性地，针对诈唬型对手

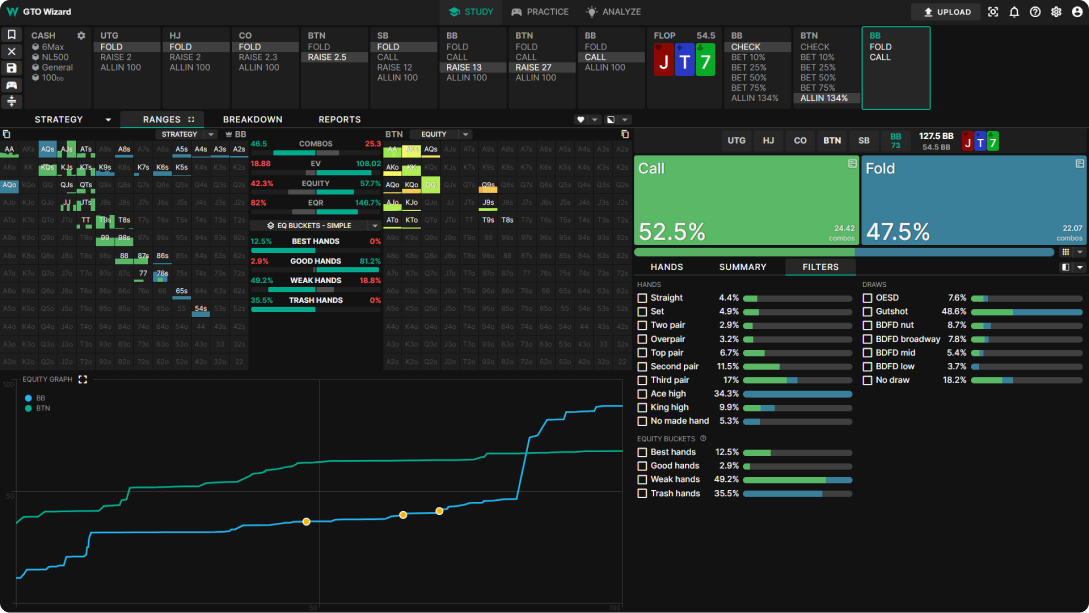
例如，这里有一个有趣的例子。这是一个 按钮位 vs 大盲注 4 下注底池，按钮位在翻牌圈全押 134%。根据 MDF，大盲注应该弃牌 134/234 = 57% 的范围，并跟注大约 43% 的范围。然而，求解器过度跟注了大约 10%！

结论

最小防守频率是用来防止对手用诈唬压制你的盾牌。Alpha 值是一把剑，用来确定你需要他们弃牌多高的频率才能证明以某个下注大小进行诈唬是合理的。

**这个指标并不完美，因为它假设诈唬没有价值。**然而，它是一个有用的指南，可以粗略地确定防守范围的宽度，或者你需要看到弃牌的大致频率。如果你认为你的对手过度或不足地诈唬，你应该策略性地进行调整。不要依赖 MDF 作为拐杖。

GTO 策略在有利位置时会密切遵循 MDF，并且在不利位置时会持续过度弃牌。（平均而言）。

这个指标显然是有价值的，并且可以应用于比我们在本文中展示的更多的方式。例如，你可以用它来确定不同路线的大致价值阈值。

希望你现在对 Alpha 值和最小防守频率的理论和应用有了更好的理解！

GTO Wizard 扑克玩家的首选应用程序

研究任何可以想象的场合

通过与 GTO 对战来练习

一键分析你的牌局

立即开始碾压 加入 Discord

作者

Tombos21

Tom 是一位资深的扑克理论爱好者，GTO Wizard 教练和 YouTuber，以及《每日 GTO 剂量》的作者。