求解器工作原理

博弈论最优求解器是一种能够计算出最佳扑克策略的算法。但这些求解器究竟是如何工作的呢？是什么让它们的策略成为“最佳”策略？

本文将深入探讨求解器的工作原理、它们所能实现的目标以及它们的局限性。

目标

在深入探讨之前，请先阅读以下两篇文章。本文旨在深入理解求解器的工作原理，如果没有一些基本的先决知识，可能会让人难以理解。如果您是求解器新手，请先阅读以下文章，然后再回到本文。

正如在什么是扑克中的 GTO？和GTO 的目标是什么？中所讨论的，GTO 的目的是实现一种不可利用的纳什均衡策略。

纳什均衡是指任何玩家都不能通过单方面改变自己的策略来获得更好结果的状态。这意味着，如果每个玩家都公开自己的策略，那么任何玩家都不会有改变自己策略的动机。这通常被描述为扑克策略的“圣杯”。但这实际上并不是求解器的设计目标。事实上，求解器并不知道“纳什均衡”是什么意思。

求解器仅仅是期望值最大化算法。

求解器中的每个代理都代表一个玩家。该玩家只有一个目标：最大化收益。问题是其他代理也都在完美地进行游戏。当你迫使这些代理互相博弈时，它们会来回迭代，利用彼此的策略，直到达到一个双方都无法改进的点。这一点就是均衡 ☯︎

GTO 是通过让利用型算法互相博弈，直到任何一方都无法进一步改进而实现的。

如何求解 GTO

• 为每个玩家分配一个均匀的随机策略（在每个决策点上的每个行动的可能性都相等）。
• 计算整个博弈树中每手牌的遗憾值（相对于对手当前策略的期望值损失）。
• 假设对手的策略保持不变，改变一个玩家的策略以减少他们的遗憾值。
• 返回步骤 2，重新计算遗憾值，然后改变对手玩家的策略以减少遗憾值。
• 重复直到达到纳什均衡。

这些循环中的每一个都称为一次迭代。所需的迭代次数从几千次到几十亿次不等，具体取决于博弈树的大小和采样方法。

步骤 1）定义博弈空间 

输入

扑克的复杂性太高，无法直接求解；我们需要使用子集和抽象来减少博弈空间，使其可计算。

通常，要运行求解器，您需要定义以下参数：

• 下注树。
• 所需的精度。
• 起始底池和筹码量。
• 起始范围（翻牌后求解器）。
• 公共牌（翻牌后求解器）。
• 翻牌后牌的抽象，例如牌桶或神经网络（翻牌前求解器）。
• 对效用函数的修改，例如抽水或ICM。

下注树的复杂性

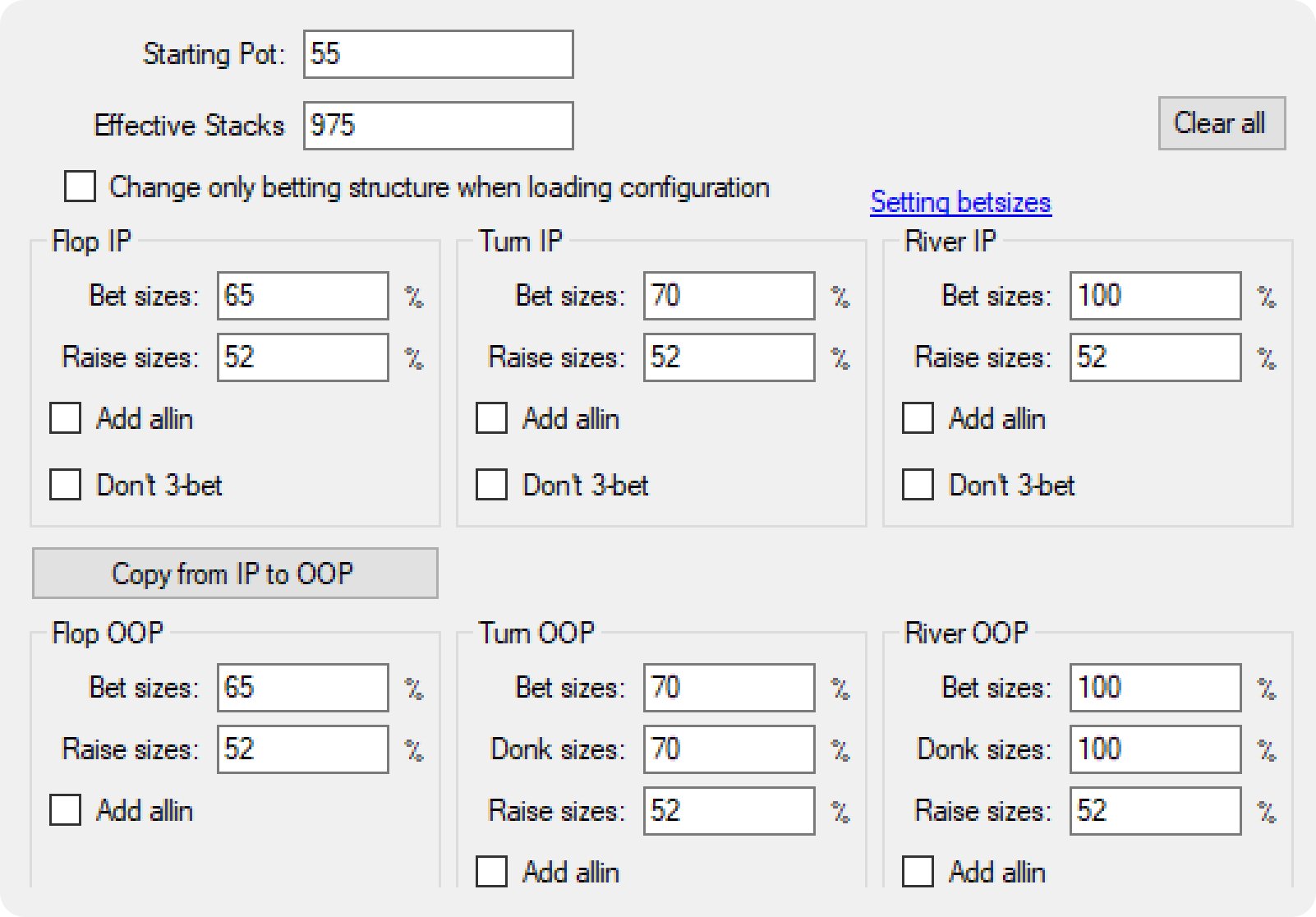
我们需要定义可用的下注尺度来减少博弈树的大小。在开始讨论算法之前，我们需要了解“下注树”是什么样的。求解器在您提供的参数范围内运行。如果您给求解器一个非常简单的博弈树，它会生成不太复杂的策略，但请记住，求解器会利用您博弈树的局限性。

求解器将生成一棵包含给定下注结构内所有可能路线的“树”。该树中的每个决策点都包含一个“节点”。例如，面对 ⅓ 底池大小的下注，OOP 的决策就是一个“节点”。树中节点的数量决定了树的大小。每个节点都需要进行优化。

像这样一棵极其简单的树有 696,613 个需要优化的独立节点。

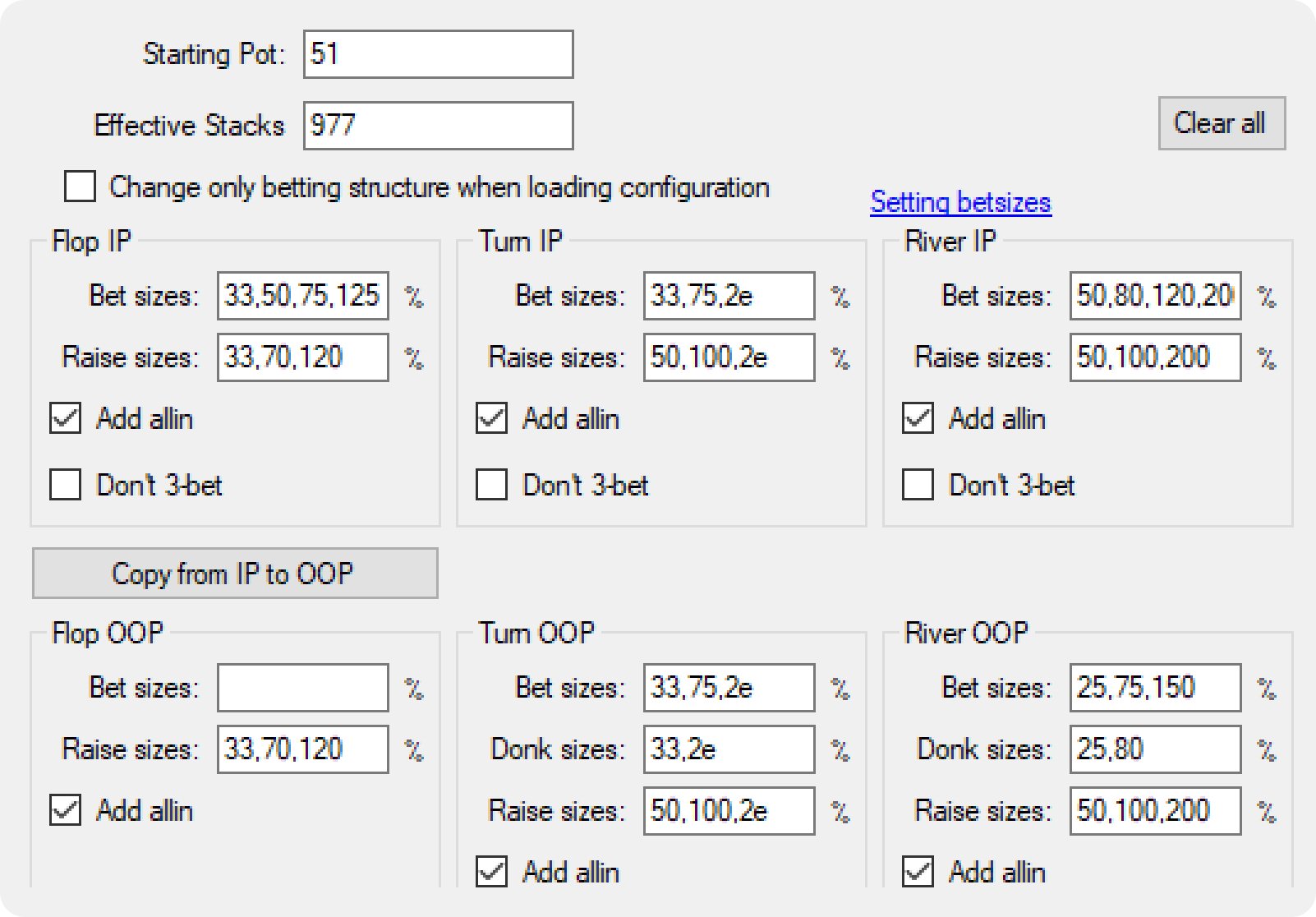
像GTO Wizard使用的那种更复杂的树包含约 87,364,678 个节点。

如您所见，复杂性会使树呈指数级增长。上面的复杂树在每个节点上使用了 4-5 倍的下注尺度，但它的大小却增加了 125 倍，求解难度也增加了 125 倍。而这仍然是对真实博弈空间的重大简化。

求解器最困难的问题之一是在当前技术的限制下优化下注树以生成可靠的策略。我们只能将树做到一定大小，否则它就会因为太大而无法求解。我们也只能将树做到一定小，否则求解器就会开始利用该树的局限性。我们正在研究寻找简化下注树的算法，以便更容易地研究扑克！这些解决方案将找到每个位置的最佳下注尺度。

GTO Wizard有许多不同类型的解决方案，例如最多 19 个下注尺度的复杂解决方案和只有几个下注尺度的简单解决方案。最终，我们发现最好先从一棵复杂的树开始，然后通过删除不常用的路线将其修剪成一棵更小、更容易管理的树。

节点锁定

GTO Wizard计划在 2023 年添加节点锁定和实时求解功能！这个强大的功能将用于探索剥削性策略和潜在的因果关系原理。

节点锁定是指在博弈树的某个节点上固定一个玩家的策略的过程。我们强迫该玩家以特定的方式进行游戏。**节点锁定通常用于开发剥削性策略！**例如，如果您强迫它在翻牌圈范围下注，那么对手玩家将最大限度地利用该策略。然而，重要的是要记住，两个玩家都会在节点锁定之前和之后进行调整以适应该锁定的节点。转牌圈和河牌圈的策略将会改变。

如果您强迫求解器进行糟糕的玩法，它会在之前和之后的节点进行修正以最大程度地减少损失。

锁定单个节点并让求解器解决该缺陷的过程被称为“最小剥削性策略”。我们不是在整个树中模拟一些漏洞，而是在树中的某个特定点进行模拟。

更复杂的节点锁定也是可能的。例如，一些求解器允许您锁定某个节点上特定组合的策略（同时让其他组合调整它们的策略）。也可以锁定许多节点来重现和利用对手策略中的更大趋势——但现代工具无法有效地适应多条街的节点锁定。

步骤 2）求解博弈树！

我们已经定义了博弈树。现在是时候求解它了！首先，我们需要了解求解器是如何计算策略的期望值的。

求解器如何计算期望值？

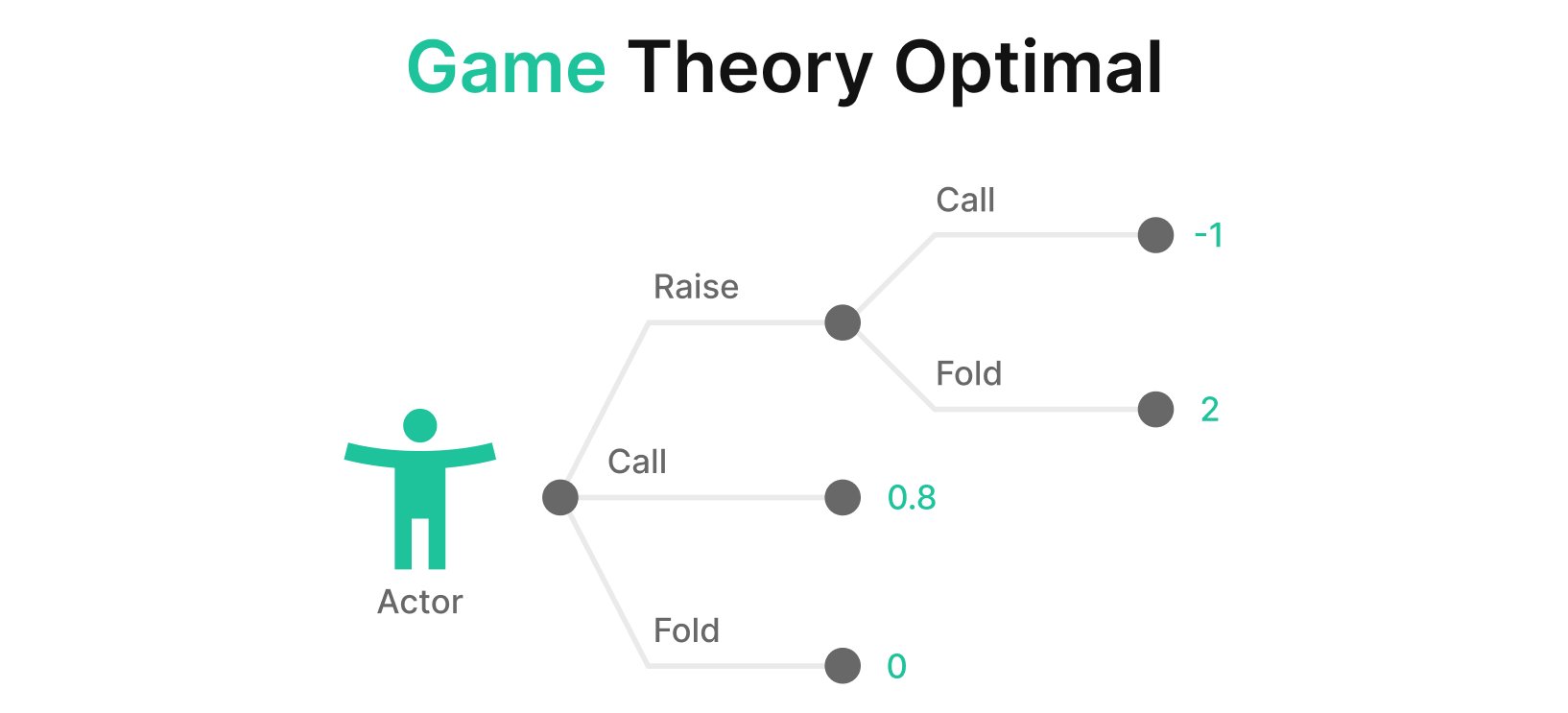
让我们想象一下上面的博弈树。每个点代表一个节点或决策点。我们如何知道每手牌在每个节点上产生了多少期望值？

这个过程很简单（对于计算机来说）。首先，我们定义终端节点（又称叶节点）。这些是牌局结束的点，要么是因为有人弃牌，要么是因为牌局进入摊牌阶段。

每个终端节点都被分配一个概率 (p) 和一个值 (x)。我们范围内的每手牌 (i) 都会产生一个单独的值和到达每个终端节点的概率。我们将每个终端节点的值和概率相乘，并将它们相加，得到总期望值。每个节点的值定义为我们赢得的总底池减去我们投入到底池中的金额。

• 从一对策略开始。
• 根据我们的策略和对手的策略，我们的牌将会以一定的频率 (p) 到达每个终端节点。
• 每个终端节点的值为 x。
• 每个终端节点的 x*p 之和就是我们的期望值 (EV)。
• 对每个节点上的每一手牌都进行此计算。

E [X] = Σxip(xi)

xi = X 取的值 p(xi) = X 取值 xi 的概率

求解器可以几乎瞬间完成这种计算。在求解器出现之前，人们使用 CREV 之类的程序来计算期望值。其局限性在于用户必须定义每个节点上的策略。因此，通常情况下，我们会将后面的节点简化为纯净的权益计算，这非常不准确。

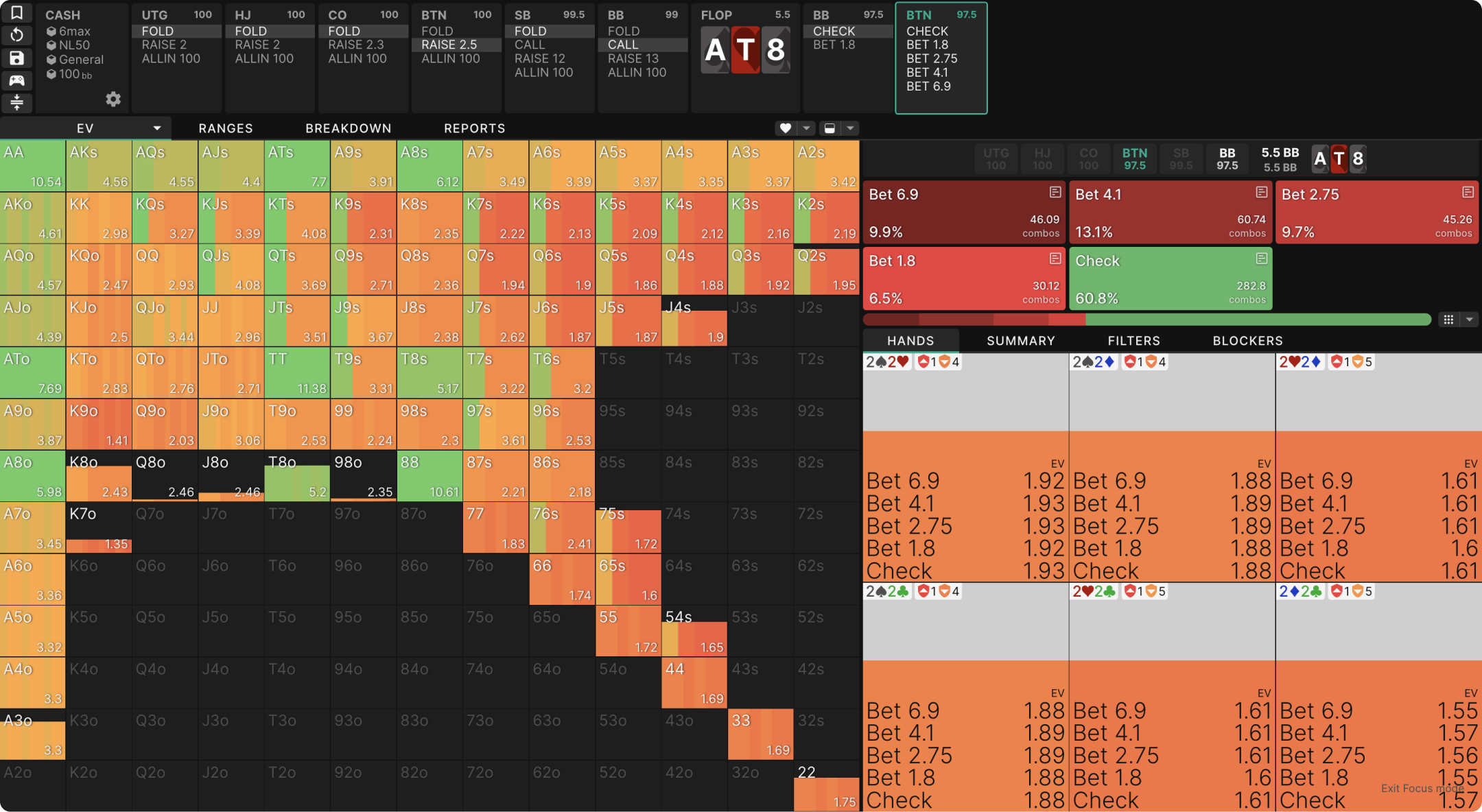
我们可以在GTO Wizard中观察到每手牌在每个点的期望值。例如，这里有一个NL50 现金游戏中 BTN vs BB SRP 的例子。我们可以看到每手牌的总体期望值（使用策略下拉菜单），将鼠标悬停在任何一手牌上都会显示我们可以采取的各种行动的期望值：

遗憾值

首先假设对手的策略是固定的（不变的）。然后，对我们在整个博弈树的每个节点上可以采取的每一个潜在行动，运行上述期望值计算。然后，我们在每个点选择期望值最高的决策，并从终端节点倒推，计算从第一个决策点开始的不同行动的期望值。

好的，我们知道了每手牌在每个节点上的价值。我们如何改进策略呢？这就是“遗憾值”概念发挥作用的地方。

最小化遗憾值是所有 GTO 算法的基础。最著名的算法叫做 CFR——反事实遗憾值最小化。反事实遗憾值是指我们对没有采取某种策略感到后悔的程度。例如，如果我们弃牌后发现跟注是一个更好的策略，那么我们会“后悔”没有跟注。从数学上讲，它衡量的是在该决策点上，采取某种行动与我们使用该手牌的整体策略相比的收益或损失。

遗憾值 = 行动期望值 – 策略期望值

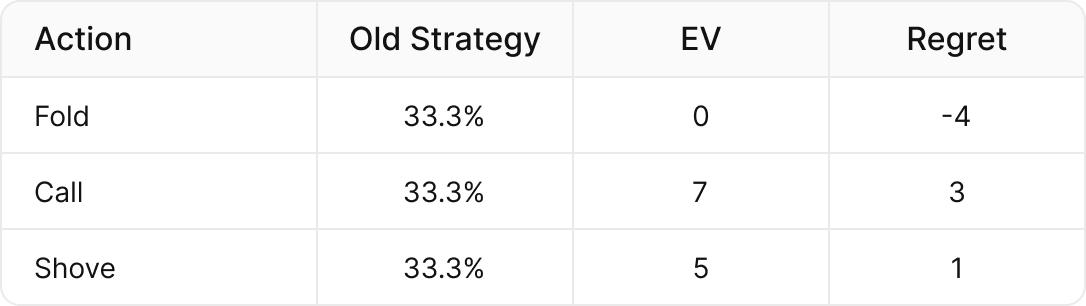
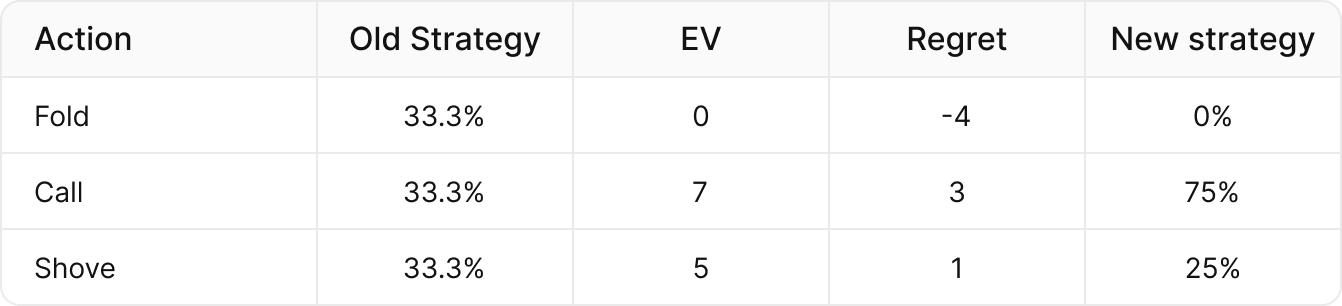
例如，如果我们当前手牌的策略是 ⅓ 的时间弃牌、跟注和全下，并且这些行动的期望值分别是（弃牌 = 0bb，跟注 = 7bb，全下 = 5bb），那么我们当前策略的期望值是：

(⅓ x 0) + (⅓ x 7 bb) + (⅓ x 5bb) = 4bb

• 弃牌的遗憾值为负，这意味着它比我们的平均策略损失更多。
• 跟注和全下的遗憾值为正，这意味着它们的表现优于我们当前的策略。

下一步是改变我们的策略以最小化遗憾值

最明显的方法是在每个决策点为每手牌简单地选择期望值最高的行动（又称最大剥削性策略）。在我们上面的例子中，这意味着总是跟注。问题是我们的对手可以改变他们的策略，这会让我们陷入循环。

例如，玩家 A 在河牌圈诈唬不足，玩家 B 弃掉所有他们的诈唬捕捉牌，然后玩家 A 总是河牌圈诈唬，然后玩家 B 跟注所有他们的诈唬捕捉牌，然后玩家 A 停止河牌圈诈唬，永远重复下去。与其在每次迭代时都完全切换到最佳应对策略，不如让每个玩家一次稍微调整一下他们的策略，朝着这个方向前进。这解决了陷入循环的问题，并且当策略对接近均衡时，收敛会更加平滑。

我们可以使用 CFR 来更新我们的策略。让我们回到之前的例子。任何遗憾值为负的行动都会停止使用。任何遗憾值为正的行动都使用以下公式：

新策略 = 行动遗憾值 / 正遗憾值之和

在我们的例子中，跟注 ->3/(3+1) = 75%，全下 ->1/(3+1) = 25%，而弃牌变为 0%，因为它有负遗憾值。

当前策略期望值 = 4.0 新策略期望值 = 6.5

请注意，这只是一次迭代。当我们多次重复这个过程时，策略将接近一个双方都无法改进的点，从而达到纳什均衡。

精度

解决方案的精度通过其纳什距离来衡量。我们从一个问题开始：

如果玩家 A 最大限度地利用玩家 B 当前的策略，他们可以赢多少？

这对计算机来说很容易计算，因为它已经知道了遗憾值。玩家 A 当前策略的期望值与其最大剥削性策略的期望值之间的差值代表了他们的纳什距离。这个数字越小，策略的可利用性就越低，精度就越高。

我们取所有玩家纳什距离的平均值来找到解决方案的精度。

只有当您在每次迭代中枚举整个策略时，这些精确的纳什距离测量才有效。大多数翻牌前求解器使用抽象和采样方法，这使得这些计算变得不切实际且不准确。像 HRC 或 Monker 这样的求解器通过测量策略/遗憾值在每次迭代中的变化程度来估计收敛性。

当纳什距离低于 1% 底池时，GTO 策略开始收敛。超过这个阈值，策略就会变得非常混合，而且往往不可靠。大多数职业玩家认为任何大于 0.5% 底池的纳什距离都是不可接受的。GTO Wizard的求解精度为起始底池的 0.1% 到 0.3%，具体取决于解决方案类型。您的博弈树越复杂，就需要更高的精度来区分相似的下注尺度。相似的尺度会导致相似的收益，因此具有许多下注尺度的更复杂的博弈树需要更高的精度才能收敛。

凸收益空间

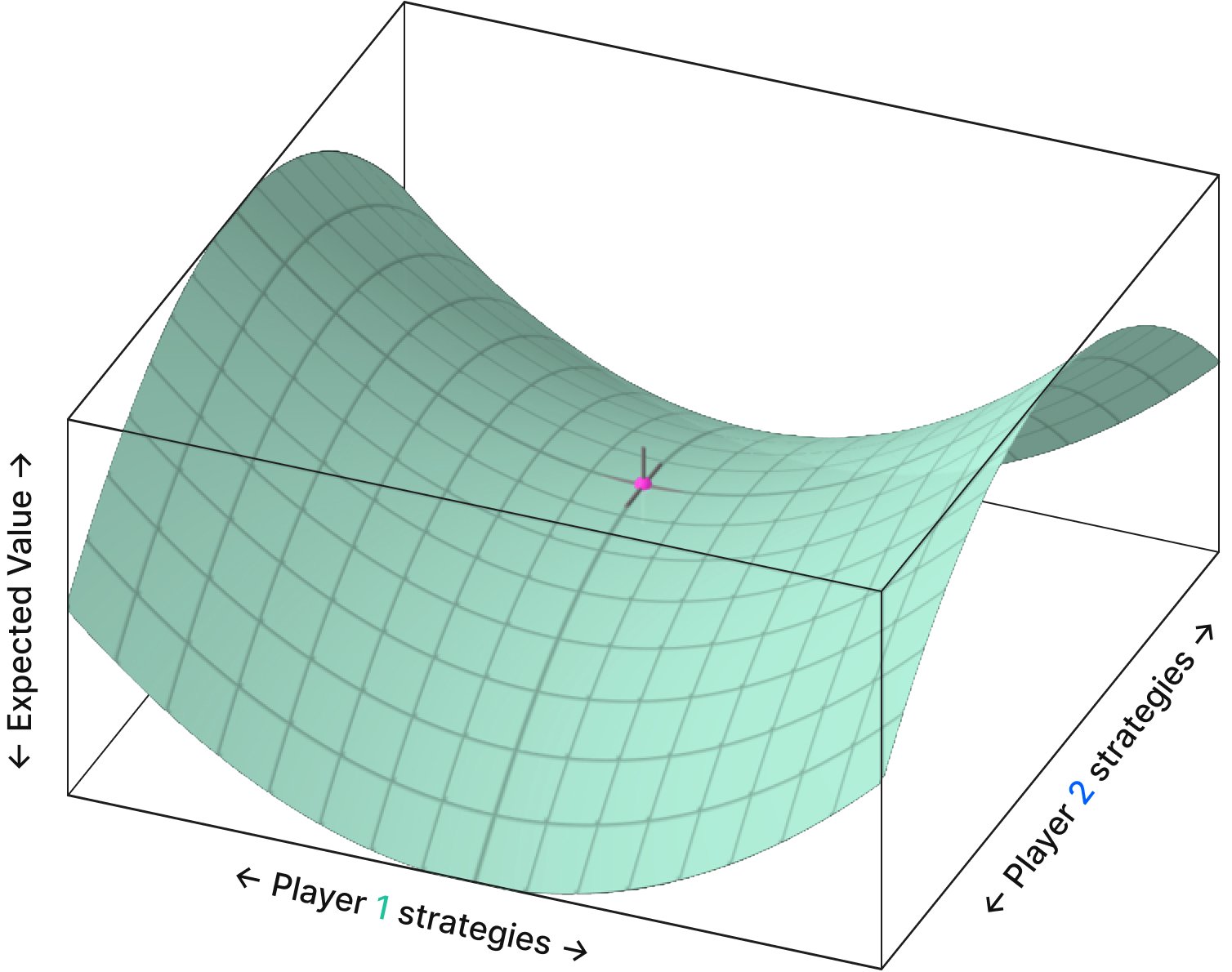
我们怎么知道这种迭代方法有效呢？我们会陷入局部最大值吗？一般来说，扑克可以被描述为一个“双线性鞍点问题”。收益空间看起来像这样：

• x 轴和 y 轴上的每个点代表一对策略。每对策略都包含关于两个玩家如何在每个回合的每个位置玩他们的整个范围的信息。
• 高度（z 轴）代表策略对的期望值，较高的点代表一个玩家的期望值优势，较低的点代表另一个玩家的优势。

大多数求解器使用一种叫做反事实遗憾值最小化 (CFR)的过程。该算法最早由 Martin Zinkevich 在 2007 年发表的一篇来自阿尔伯塔大学的论文中提出。该论文证明了 CFR 算法不会陷入某个局部最大值，并且只要有足够的时间，就会达到均衡。

这个鞍点的中心代表纳什均衡。图上没有曲率的点——这意味着任何一个玩家都不能通过改变他们的策略来提高他们的收益。

延伸阅读

• 我们强烈建议您阅读这篇文章，以了解更多关于扑克中 CFR 的信息。
• 这个网站提供了一个很棒的教程和构建简单 CFR 算法的分步说明。
• 关于在扑克中使用 CFR 的学术资源。
• 深度 CFR——应用神经网络来加速 CFR 计算。
• 使用“折扣”遗憾值最小化改进原始 CFR 算法。

结论

呼，信息量真大！希望到现在为止，您对求解器的实际工作原理有了更好的理解。让我们回顾一下要点：

• 出于所有实际目的，主要的收获是，求解器是期望值最大化算法，它们利用我们提供的博弈树。
• 求解器算法生成最大剥削性策略。让这些算法互相博弈会产生不可剥削的均衡策略。
• 计算一对策略的期望值是容易的部分（对于计算机来说）。将策略朝着正确的方向调整并无数次地迭代这个过程才是困难的部分。
• 扑克太复杂了，无法直接求解，因此我们使用抽象技术（例如限制下注尺度）来简化博弈空间。
• 求解器的精度取决于您给它们的抽象博弈。过于复杂则无法求解，而且人类也难以从中学习。过于简单则会导致求解器利用该博弈树的局限性。

GTO Wizard  扑克玩家的首选应用程序

 研究任何可以想象的位置

通过与 GTO 对战来练习

一键分析您的牌局

立即开始碾压对手加入 Discord

作者

Tombos21

Tom 是一位资深的扑克理论爱好者、GTO Wizard 教练和 YouTuber，以及“每日 GTO”的作者。