方差和资金管理

每个扑克玩家必备的软技能

尽管我们尽最大努力在牌桌上最大化我们的优势，但从本质上讲，扑克仍然是一种赌博游戏。它是可以战胜的，但它仍然建立在与其他所有赌场游戏相同的基石之上：疯狂的、令人心碎的、令人麻木的方差！

观看视频

扑克是运气🍀还是技巧？

两者都是！运气和技巧的比例取决于你玩了多少手牌。微小的优势会在长期内被放大。在短期内，你的结果主要取决于运气。但即使是很小的优势，在足够长的时间线上也会变得不可避免。你的结果在短期内主要受运气支配，在长期内则受技巧支配！

方差究竟是什么？

方差是指对数据集中数字之间离散程度的统计度量。在扑克中，方差指的是你的结果有多“波动”！

在方差较高的游戏中，玩家的结果在给定样本中的偏差会更大。

方差是用“标准差”指标来衡量的。你可以在大多数扑克 HUD 中找到这个指标，但它也可以直接从你的结果中计算出来。对于现金游戏，这是以 BB/100 来衡量的。

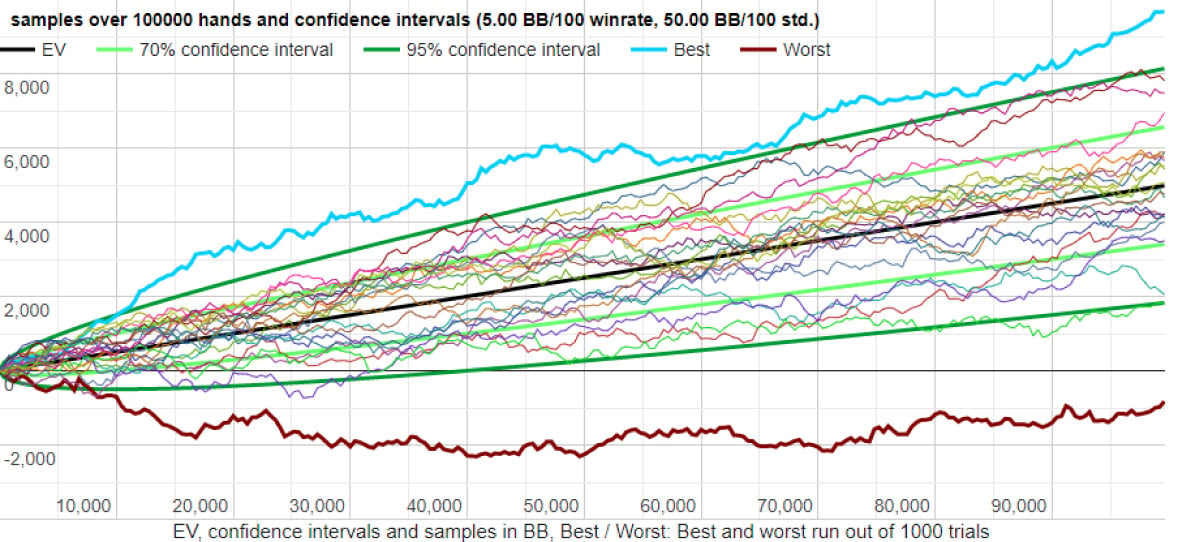
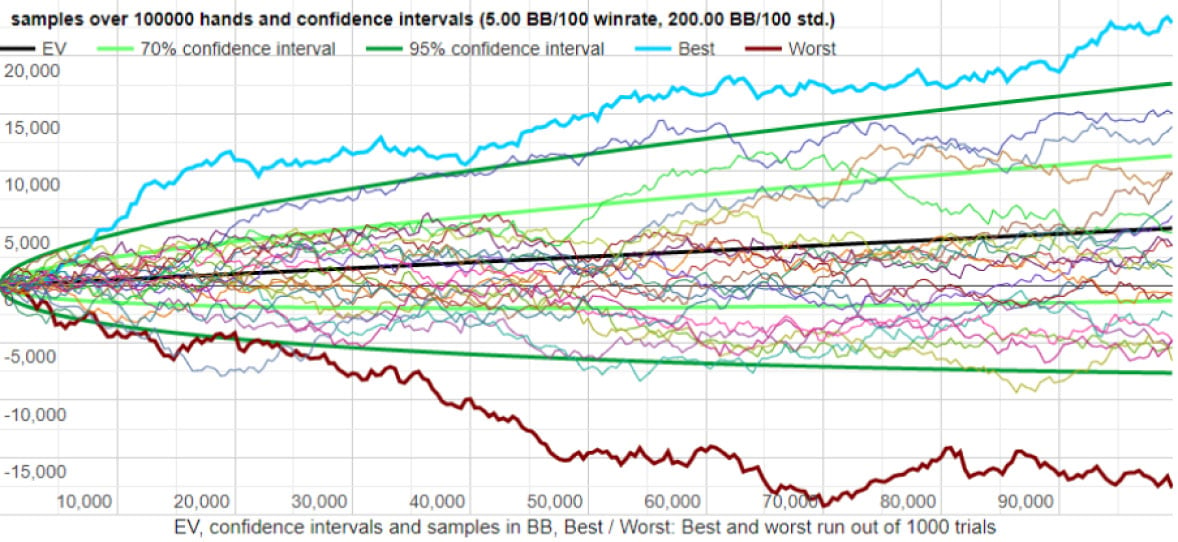
让我们来看一些例子。以下图表是在一组给定输入下 20 次随机运行的示例 (来源：Primedope)

低方差结果

请注意，最好和最差的运行结果介于 -1,000 BB 和 +10,000 BB 之间。

高方差结果

请注意，最好和最差的运行结果介于 -17,000 和 +22,000 之间！

两位玩家的胜率相同，但方差较高的玩家的最好和最差运行结果之间的差距要大得多！

大数定律

赌徒谬误在扑克玩家中非常普遍。假设我们抛一枚公平的硬币，它连续 6 次正面朝上。那么下一次抛硬币正面朝上的概率是多少？

如果你迷信，你可能会认为你“应该”得到反面。但这根本不是现实的运作方式。下一次抛硬币仍然是 50%/50%。你抛出第 7 次正面的可能性和你第一次抛出正面的可能性一样大。

在抛掷数千次之后，我们预计正面和反面出现的次数会趋于平衡。但这并不是因为某种普遍的因果报应；这仅仅是大数定律。想象一下，我们抛掷 1000 次，正面仍然保持 6 次的领先优势。此时，我们抛出了 503 次正面和 497 次反面——这实际上是从 6 分领先开始时的期望值。此时，正面出现的概率是 50.3%，反面出现的概率是 49.7%。

现在想象一下，我们抛掷 100,000 次，并保持同样的 6 分领先优势。现在正面出现的概率是 50.0003%，反面出现的概率是 49.9997%。“运气”似乎趋于平衡，尽管反面从未赶上。这就是大数定律。

同样，仅仅因为你运气不好，并不意味着你“应该”得到好运。牌组不欠你任何东西。每一手牌都是一个独立的事件，不会记住你的 AA 是如何被爆冷的。

反之亦然。仅仅因为你运气好，并不意味着你“应该”得到坏运气。事实是，扑克中的方差远远超出了人类真正能够理解的范围。如果你曾经玩过扑克方差计算器，你会发现你需要玩数万手牌才能看到统计上显著的优势显现出来。

置信区间

我们看到的最常见的问题之一是“我需要玩多少手牌才能确定我的胜率？”。这个问题的问题在于它没有真正的答案。在数学中，我们使用置信区间来处理这些未知数！

置信区间遵循 68-95-99 规则：

• 68% 的情况下，你的结果将落在均值的 1 个标准差 σ 范围内
• 95% 的结果落在均值的 2 个标准差 (2σ) 范围内
• 99.7% 的结果落在均值的 3 个标准差 (3σ) 范围内

方差分布

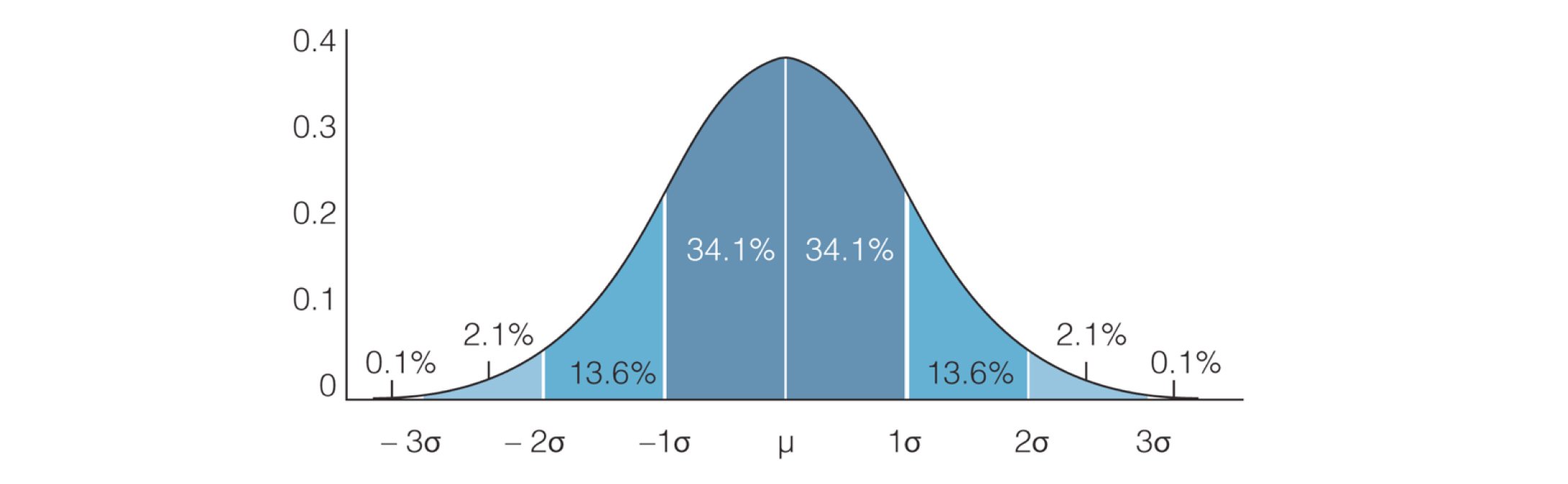
μ = 期望值

-1σ 到 1σ = 1 个标准差（即：约 2/3 的情况下，你的结果将落在该范围内）-2σ 到 2σ = 2 个标准差（即：95% 的情况下，你的结果将落在该范围内）-3σ 到 3σ = 3 个标准差（即：99.7% 的情况下，你的结果将落在该范围内）

让我们来看一个例子：

假设你的“真实”（平均）胜率是 2.5 BB/100。这是你的期望值。你在 100k 手牌后的标准差 (σ) 是 3.16 BB/100。一种更好的写你的胜率的方法是：

2.5 ± 3.16 BB/100。（胜率 ± σ）

换句话说：

• 70% 的情况下（约 1σ），你的结果将落在 -0.66 BB/100 和 5.66 BB/100 之间
• 95% 的情况下（2σ），你的结果将落在 -3.82 和 8.82 BB/100 之间

在科学中，未知变量会被赋予误差范围和置信区间，而不是精确的数字。你的胜率是一个未知变量。因此，不可能给出一个确切的数字。你能做的最好的事情就是给出一些误差范围。

误差范围的公式是标准差和样本量的函数。增加样本量或降低方差将降低误差范围并提高结果的可信度。公式如下：

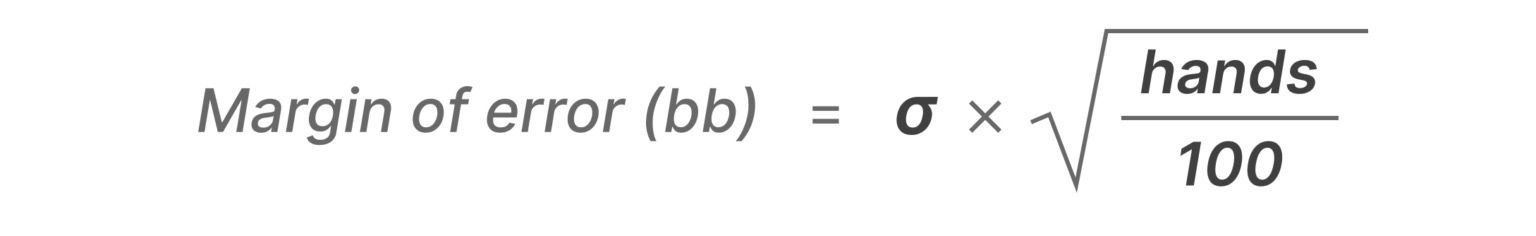
其中 σ 是你的标准差（以 BB/100 为单位），hands 只是你玩过的牌数。例如，上面我们看到标准差为 100 BB/100，玩了 100k 手牌。100 * (100,000/100)^0.5 = 3162。换句话说，结果是正负 3162 BB，或 3.16 BB/100。这在上面的图片中显示为“100000 手牌后的标准差”，但更容易将其视为误差范围。

管理风险

方差可以通过免费的计算机程序根据上述输入来计算。

推荐的一些网站是 Primedope 和 ReviewPokerRooms。了解方差的界限是将你的结果和预期放在具体环境中考虑的好方法。花一些时间自己尝试不同的输入并查看结果的输出是非常宝贵的。

以上工具适用于现金游戏 💸。MTT 玩家往往会经历更大的方差。试试这个 MTT 方差计算器！

资金管理指南

本文的目的是为你提供构建自己的资金管理策略的工具，而不是规定某个答案。你的资金管理是你的风险偏好的函数。但是，我们根据常识概述了一些非常基本的资金管理指南：

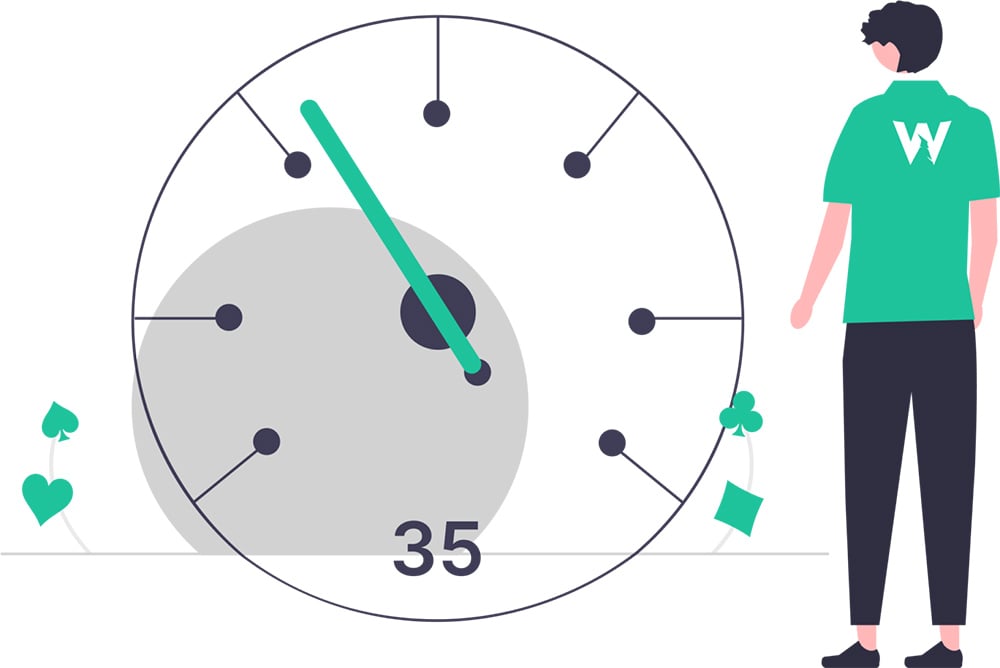
对于现金游戏玩家：35 到 65 个买入

• 永远不要冒超过你资金 5% 的风险

对于锦标赛玩家：75 到 125 个买入

• 永远不要冒超过你资金 2% 的风险

凯利准则

凯利准则告诉你应该冒你资金的多少风险。它考虑了你在一次投注中的优势和赔率，并输出你应该冒你资金的多少风险。

“资金管理策略的核心是在不透支资金的情况下最大化你的优势。这就是凯利准则的作用。”

凯利准则的公式如下：

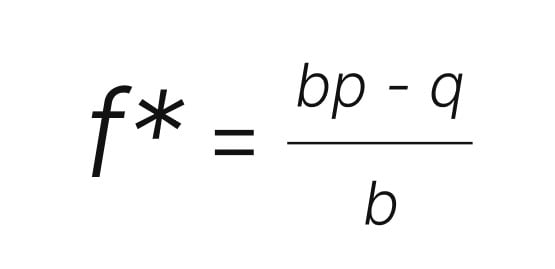
f = 资金中应该下注的部分 b = 十进制赔率 – 1 p = 获胜的概率 q = 输的概率，即 1 – p

  让我们来看一个例子

你玩 HU SnG，平均投资回报率 (ROI) 为 5%。你的资金是 1000 美元。你应该玩什么级别的比赛才能尽可能快地增加你的资金？

A) 100 美元买入 B) 50 美元买入 C) 25 美元买入 D) 10 美元买入

🎲 答案

B) 50 美元买入

凯利准则的基本前提是你应该冒你优势的风险！对于一个简单的 1:1 的赌注，如果你有 5% 的优势，你应该冒你资金的 5% 的风险，在这个例子中是 50 美元。

以下是使用数学方法解决此问题的方法：

b = 1 p = 52.5% q = 47.5% f* = p – q = ROI f* = 5% 1000 美元的 5% = 50 美元

这是基于“完全凯利”策略。完全凯利策略就像让你的引擎超负荷运转！在实践中，通常最好采用半凯利甚至四分之一凯利策略。半凯利策略可以获得 75% 的增长，而只承担 25% 的方差。所以在实践中，C) 25 美元买入可能是更好的答案。

最佳资金管理策略

凯利准则告诉你应该冒你资金的多少风险。你应该冒多少风险取决于你的胜率和方差。请记住，凯利准则是边界，而不是目标！在实践中，你应该投资少于凯利准则建议的金额。

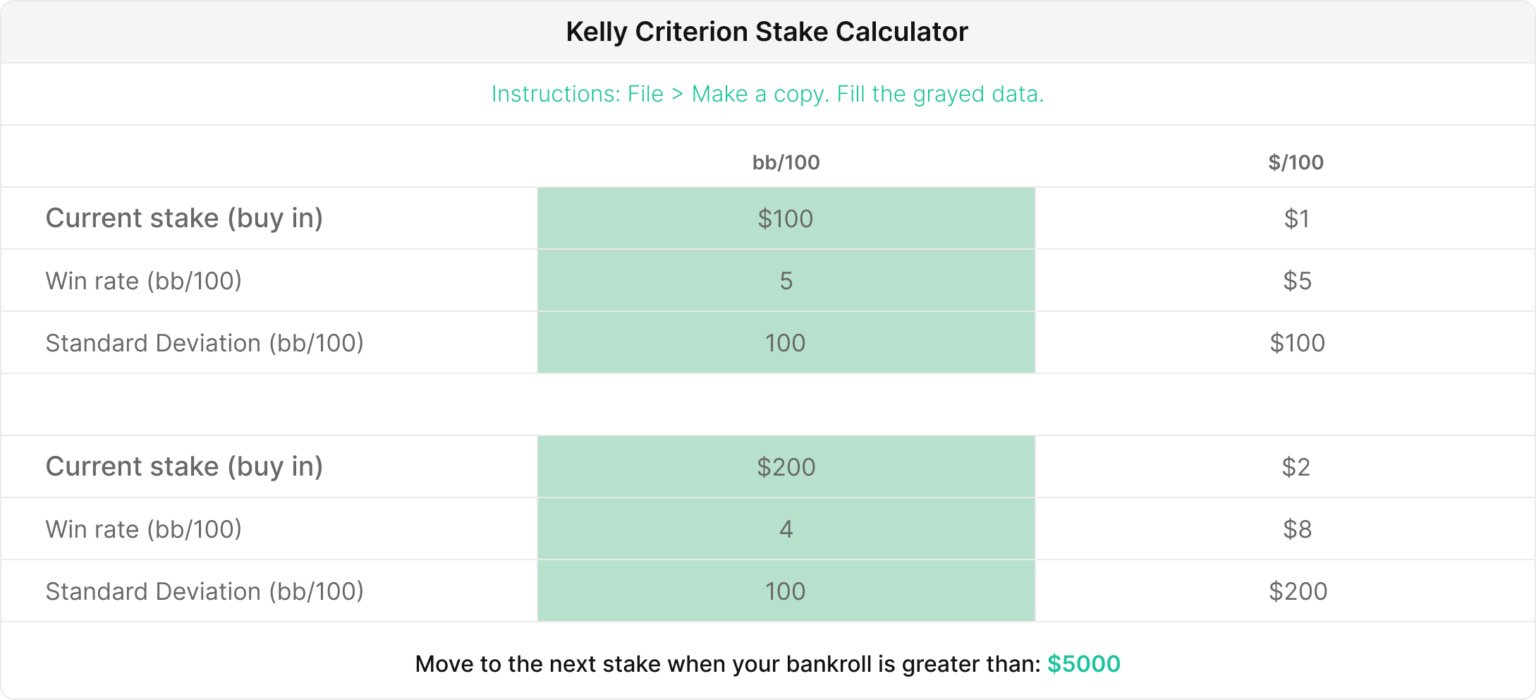
我们可以使用数学方法将现金游戏或其他形式的扑克胜率转换为最佳资金管理策略。我们构建了一个方便的资金管理优化工具来帮助你更快地升级！ 💪

这个计算器 可以找到最低资金要求，以证明升级级别并承担更多方差以换取更高的每小时胜率是合理的。

我们还包含了一个（测试版）MTT 玩家计算器！对于具有多个结果（锦标赛名次）的投注，凯利准则变得更加复杂。有些结果会导致你的资金发生巨大变化，而另一些结果则很小。

最大化此等式以找到 MTT 中的最佳资金管理策略：

f(x) = 概率₁log(结果₁) + 概率₂log(结果₂) + 概率₃log(结果₃) + …

其中：

• 概率表示在锦标赛中获得每个名次的概率。
• 结果表示你在锦标赛中获得某个名次后资金的分数变化。例如，如果获得第一名会使你的资金增加 20%，那么该结果的值将被指定为 1.2。如果出局会使你的资金减少 1%，那么该结果的值将被指定为 0.99。
• 为事件中的每个可能结果添加一个术语。

在实践中，很难为这个等式赋值，但我们可以根据一些优势 (ROI) 来估计概率。请注意，对于大多数大型 MTT 来说，100 个买入的规则过于激进！

上头

上头的定义是由于情绪困扰而不是理性判断而采取的次优行动。许多扑克玩家在下风期时会屈服于上头，因为他们害怕输掉更多的钱或渴望赢回之前的损失。

上头可能非常危险，因为如上所述，降低你的胜率会导致更大的方差。这会成为一个自我实现的预言，并进一步延长下风期的持续时间。

我们将在后面的文章中详细讨论上头管理。

结论

如果说从研究扑克方差中可以学到一件事，那就是那句古老的格言“不要用你输不起的钱去赌博”是正确的。

我们希望，随着你更多地了解方差，它将帮助你更好地理解上风期和下风期的暂时性，并在你的扑克之旅中提升你的心理状态。

GTO Wizard  扑克玩家的首选应用程序

 研究任何可以想象的场合

通过与 GTO 对战来练习

一键分析你的牌局

立即开始碾压加入 Discord

作者

Tombos21

Tom 是一位资深的扑克理论爱好者、GTO Wizard 教练和 YouTuber，以及《每日 GTO 剂量》的作者。