一道组合数学题

今天我们为您准备了一个特别的题，它将测试您作为一名扑克玩家的直觉，并挑战您对组合数学的理解。

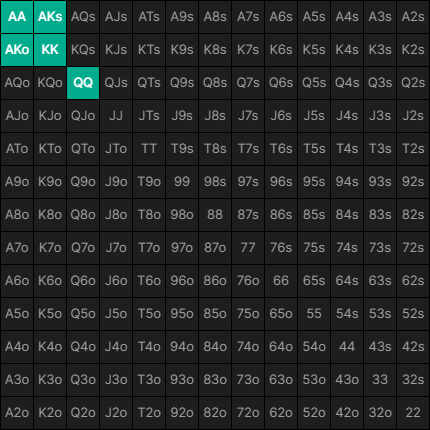
六名玩家翻牌前全押，范围为 (QQ+，AK)。

问题：

• QQ 能赢得底池吗？如果可以，怎么做？
• KK 能赢得底池吗？如果可以，怎么做？
• 在这种情况下，您更愿意持有 QQ、KK 还是 AKo？
• 一名旁观者进行了一项边注。如果翻牌后公共牌出现任何 A/K/Q，他们将赢得边注。他们获胜的几率是多少？

请注意，您不需要赢率计算器或任何特殊软件来回答这些问题。

答案：

正确答案

回答这些问题的诀窍是问问自己，6 个不同的玩家最终拿到符合这些范围的牌的可能性有多大。 当您考虑牌的移除效应时，可能性就变得非常有限。

牌堆中只有 12 张牌包含 Q、K 或 A。 6 名玩家每人两张牌将用掉牌堆中所有的 K、Q 和 A。

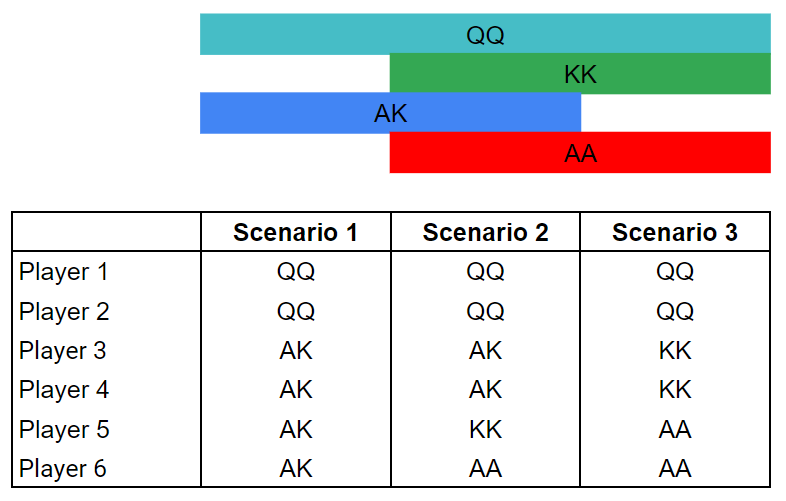
现在让我们来看看 6 名玩家拿到符合这些范围的牌有多少种方式。只有 3 种可能性：

QQ 能赢得底池吗？如果可以，怎么做？

是的，但前提是它组成同花顺！ 在所有情况下，必定有两名玩家持有 QQ。所有 A 和 K 都被玩家持有了，所以用同花获胜是不可能的。所有的 Q 都被玩家持有了，因此不可能胜过更大的对子。

KK 能赢得底池吗？如果可以，怎么做？

不，KK 不能赢得底池。KK 总是需要击败 AA 才能获胜。要做到这一点，它必须组成顺子、同花或拿到第三张 K。由于所有 K 都已被玩家持有，因此不可能拿到第三张 K。由于所有 Q 都已被玩家持有，因此不可能组成顺子。所有的 A 都被玩家持有了，所以它不能用同花获胜。因此，KK 不能赢得底池。

在这种情况下，您更愿意持有 QQ、KK 还是 AKo？

QQ 的赢率比其他牌要高得多。获胜不仅仅是赢得底池的唯一方式，您还可以平分底池。⅓ 的情况下 QQ 会出现在场景 1 中，您将面对另一个 QQ 和 4 个持有 AK 的玩家。这对 QQ 来说非常有利可图，因为 AK 会阻挡彼此的 outs。

KK 唯一平分底池的方式是所有 6 名玩家通过公共牌上的最小顺子平分底池。

AK 总是会面对 1 个或 3 个其他 AK。它可以用 A 做成同花获胜，也可以用最小顺子平分底池。然而，与 QQ 1/3 的几率遇到场景 1 相比，这些事件发生的可能性要小得多。

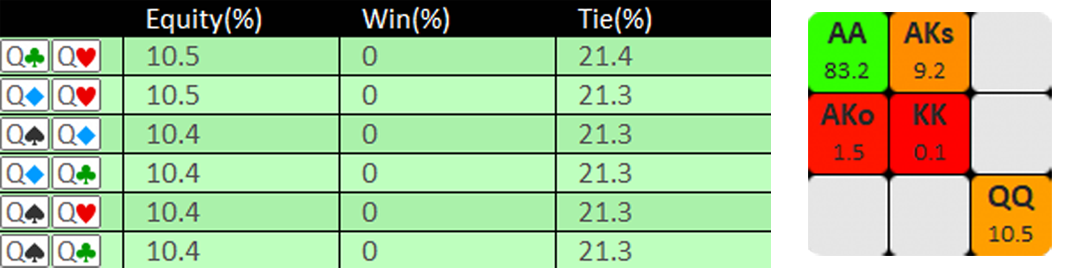
如果我们进行一个简单的赢率计算，我们会发现 QQ 的赢率比 KK 或 AKo 高得多。然而，这是因为 QQ 在超过 20% 的情况下会与其他 QQ 平分底池。

一名旁观者进行了一项边注。如果翻牌后公共牌出现任何 A/K/Q，他们将赢得边注。他们获胜的几率是多少？

概率恰好为零，因为所有的 A、K 和 Q 都必须由 6 名玩家持有。

GTO Wizard 扑克玩家排名第一的应用程序

学习任何牌局

通过对抗 GTO 练习

一键分析你的牌局

立即开始制胜 加入 DISCORD

作者

Tombos21

Tom 是一位长期扑克理论爱好者、GTO Wizard 教练和 YouTuber，以及《GTO每日技巧》的作者。